企業合同プロコンを主催しました

AI事業本部の西山です。先月11/19火曜日、私が所属するプロコンゼミのメンバーで企業合同プロコンを実施しました。企業合同プロコンは、社会人の競技プログラマー達が集まり、企業横断の混合チームを作ってプログラミングコンテストを行うイベントで、四半期に一度程度の頻度で行っています。今回は全25社、総勢53名の競技プログラマーが集まり、プログラミングコンテストを行いました。

本ブログでは企業合同プロコンの様子を紹介します。

プロコンゼミとは

企業合同プロコンについてお話する前に、プロコンゼミについてご紹介します。

CyberAgentにはゼミ制度という、業務時間の一部を研究や技術の向上に使うことができる制度があり、プロコンゼミもその一つです。プロコンゼミは、競技プログラミングを通して技術課題への向き合い方を習得することを目的としたゼミで、2019/04から活動を開始し、現在まで継続して行なっています。

メンバーは10人を超え、AtCoderのレート換算で黄色から茶色まで幅広くいますが、ボリュームゾーンは緑です。主な活動は直前のコンテスト（主にAtCoder）の振り返りで、この振り返りではメンバーに単に解説してもらうだけでなく、どのような思考過程を経て答えにたどり着いたかを説明してもらっています。より高みを目指し、毎週精進を続けています。

企業合同プログラミングコンテスト

企業合同プログラミングコンテストは、社会人競技プログラマーからなるコミュニティで実施されているイベントで、四半期に一度程度行われています。会場は提供可能な企業が持ち回りで提供しています。

最近では参加人数が50人を超え、広い会場が必要となっているとの相談を受け、弊社の渋谷スクランブルスクエアのセミナールームで主催をしてみました。これまでのイベントスケジュールを参考にし、以下のようなスケジュールで実施しました。

• 19:00 ~ 19:55 開場 & 懇親会
• 19:55 ~ 20:00 コンテスト準備
• 20:00 ~ 22:00 コンテスト
• 22:00 ~ 22:30 結果発表 & 解説
• 22:30 ~           解散

ここからはコンテスト当日の様子を紹介します。

懇親会

コンテストの前の1時間で懇親会を行いました。今回はピザと寿司、飲み物を用意しました。

こちらが懇親会の風景です。ご飯を食べながら談笑したり、コンテストに向けた準備をしたり思い思いに過ごしていました。2枚目のオレオはuwiさんからいただいたお土産です。直前までTCO19に競技者として参加しており、そのお土産とのことでした。ごちそうさまでした。

コンテスト

コンテストはイベント参加者の53人で、企業横断の5~6人チーム10チームに分かれ、全12問の問題の解答数と解答時間を競いました。コンテストの問題はuwiさんにご協力いただいて用意しました。uwiさんありがとうございました！ 実際のコンテストに利用した問題セットはこちらになります。

https://codeforces.com/gym/102152

企業合同プロコンの醍醐味は、企業横断の混合チームでのICPC形式のコンテストにあります。今回は事前に登録していただいた内容からAtCoderレートを調べ、チームのレート平均の差がなるべく小さく、かつ同チームに同企業の競技者がなるべく含まれないように調節をしました。
チーム分けの結果、各チームのレート平均は1600~2400の間になり、非常にレベルの高い混合チームとなりました。

コンテスト結果

2時間にわたるコンテストの結果、ほぼ全チームが2時間で12問全完し、解答速度で競うコンテストになりました。優勝はcaprocon_team1で、なんと1時間弱で全12問を解き切る驚異の成績を叩き出しました！

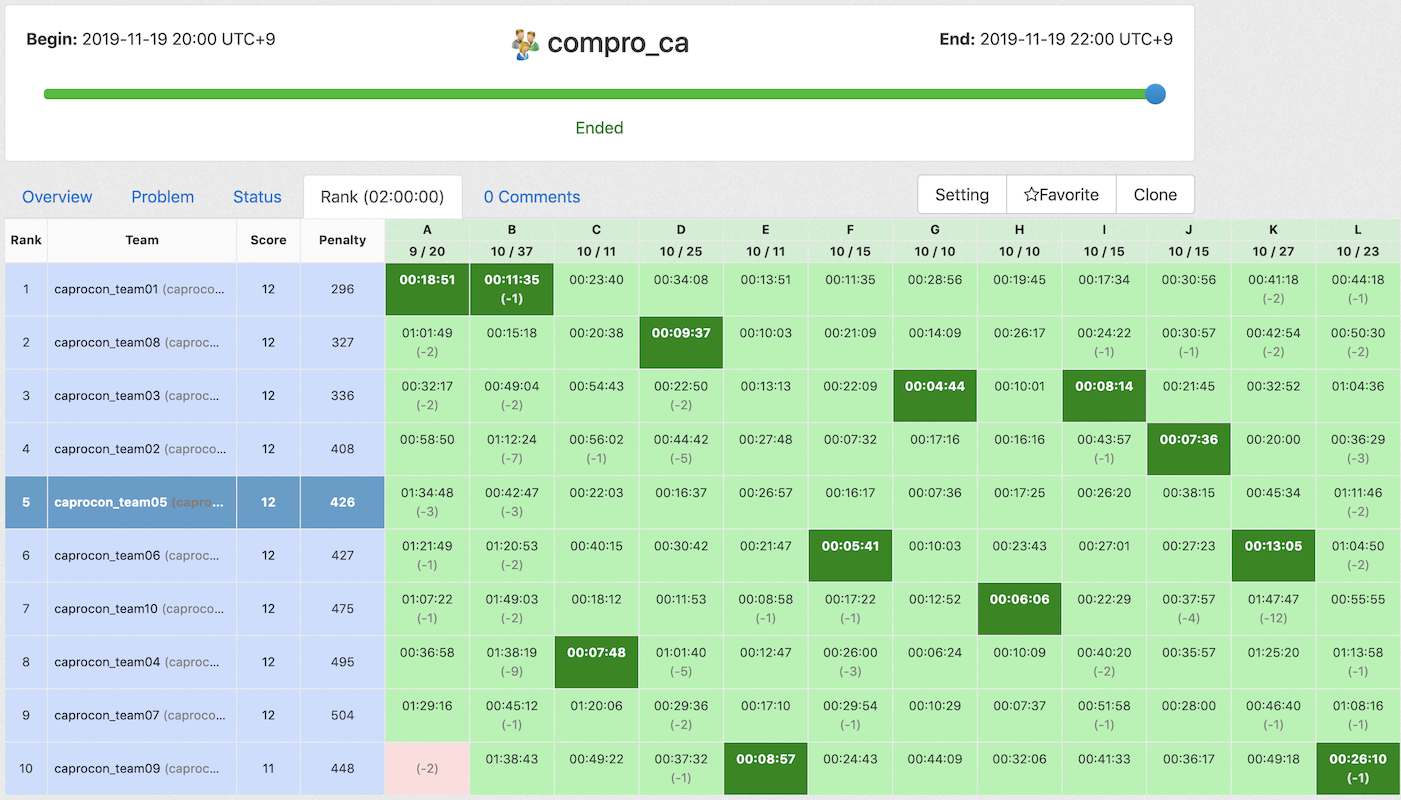
　今回のセットは難易度が低いセットでしたが、AとLは少し難しい問題で、どのチームも苦戦されていたようです。

解説

コンテスト結果発表後、問題の解説を各問題で最初のAcceptを獲得したチームにしていただきました。ホワイトボードに図を書きながら説明してもらいました。

印象に残った問題を一問紹介します。

L Median

問題概要

　N行M列のマスに1 ~ N * Mまでの数字が一つずつ入力されています。ここで、追加でHとWが入力として与えられます。N行M列のマスに含まれるすべてのH行W列の長方形それぞれに対し、内包される数字の集合の中央値を列挙したとき、その最小値を答えてください。

問題制約

1 <= M, N <= 1,000
1 <= H <= N, 1 <= W <= M
HとWは奇数

解法

愚直に実装すると、N * M マスに内包されるすべてのH * Wマスの長方形に対し、中央値を計算してその最小値を取ることで答えを出すことができます。しかしこれでは、最悪O(NMHW log HW) > 10^12 となり、到底制限時間内に答えを出すことができません。

そこで、中央値となる条件についてもう少し考察を進めてみます。中央値がmedならば、H * Wの長方形内に[1, med)の整数をちょうどH * W / 2個含むことになります。
ここである整数Xについて、すべてのH * Wの長方形に[1, X]のいずれかを中央値とする長方形がないならば、それぞれの長方形に含まれる[1, X]までの数の個数は H * W / 2以下になります。すなわち、問いの答えとなる中央値は[X + 1, N * M]の間にあることがわかります。逆に、どれか一つでも[1, X]までの数の個数がH * W / 2個を超える長方形が見つかれば、問いの答えとなる中央値の候補は[1, X]にあることがわかります。
あるXに対し、「[1, X]の整数を H * W / 2 を超える個数含む長方形が存在するかどうか」がわかれば、問いの答えの範囲を絞れるということは、この問題には二分探索が利用できます。この計算量はO(log NM) になります。

肝心の「[1, X]の整数を H * W / 2 を超える個数含む長方形が存在するかどうか」ですが、あるマス (x, y) について、(x, y) を左上とするようなH * Wの長方形に[1, X] の整数が何個含まれるかを数え上げていけば良いです。
例えば次図のようなX = 5, (H, W) = (3, 3) のケースを考えます。

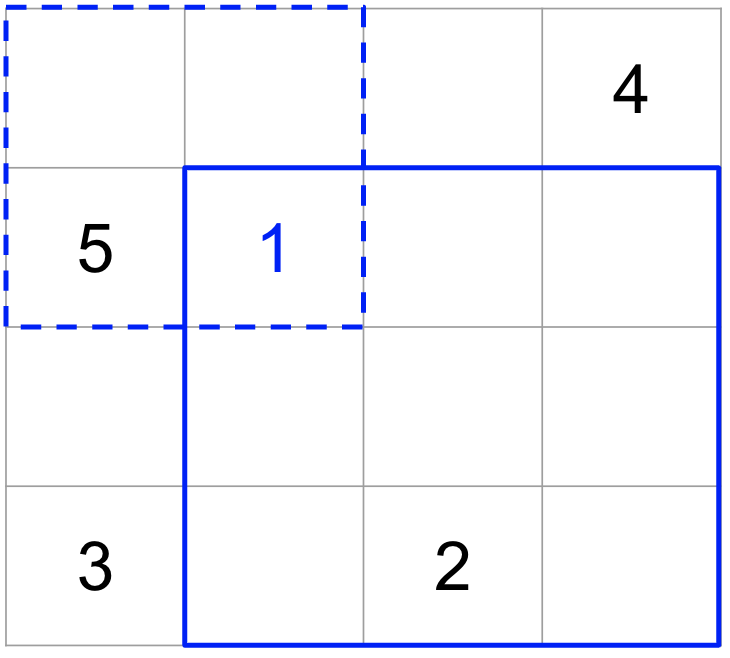
青の1に注目すると、点線の青い四角の領域内にH * Wの長方形（青実線四角形）の左上のマスがあれば、それらの長方形は青の1を含むことがわかります。この結果を次図のように、対応するマスを左上とする長方形が[1, X] を含んだ個数として別の表にメモしておきます。

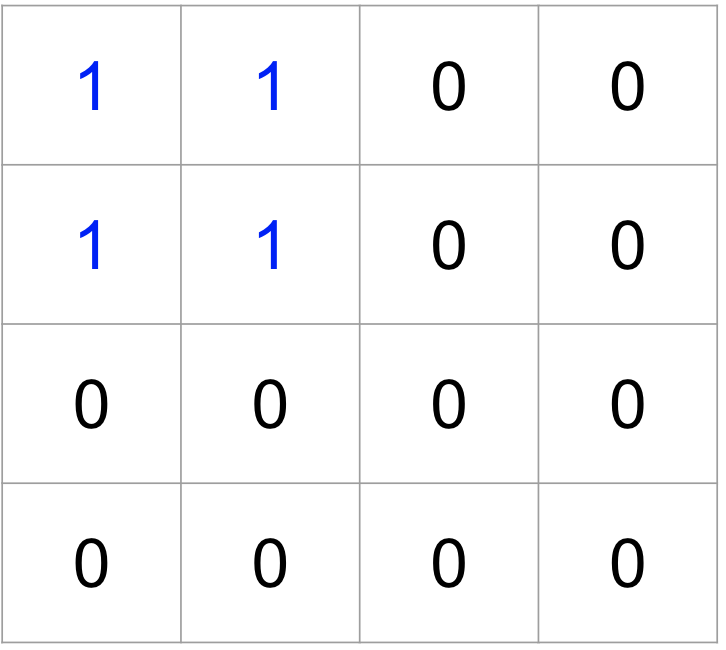
この操作を[1, 5] のすべてに対して行い、最終的に次図の表を得ると「[1, X]の整数を H * W / 2 を超える個数含む長方形が存在するかどうか」判定できるようになります。

これは2次元のいもす法（ https://imoz.jp/algorithms/imos_method.html ）を活用することでO(NM)で作成でき、判定も同じオーダーで行えるので合わせてO(NM)になります。
以上から、O(NM log NM) でこの問題を解くことができ、現実時間内で解を出すことができます。

解答はこちら: https://codeforces.com/gym/102152/submission/66879675

まとめ

私たちプロコンゼミは、企業合同プログラミングコンテストを主催しました。主催にあたって会場準備は思った以上に大変でしたが、アンケートの結果からは多数の方に満足していただけたことがわかり嬉しく思います。
私たちCAのプロコンコミュニティはまだ発足したばかりですが、今後もCAのプロコンゼミとして、社外のコミュニティにも関わっていこうと思います。