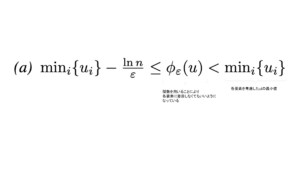はじめに

本記事は、CyberAgent Advent Calendar 2022 10日目の記事です。

技術本部 Data Science Center (DSC) の中野（@nanay_desu）です。

NeurIPS 2022に採択された「Online Algorithms for the Santa Claus Problem [1]」を紹介しようと思います。

ざっくりまとめたので、時間のない方はこのスライドだけ見ていただければと…

目次

1. サンタクロース問題について
2. オフラインからオンラインのストーリー
3. オンラインサンタクロース問題
   1. オンライン問題の入力のモデル
   2. オンラインアルゴリズムの評価
4. 研究の成果
   1. すごいPoint: Greedyな方法だが、全体を上手に考慮したようなアルゴリズムになっている
   2. すごいPoint: 前半と後半に分ける
5. 実際に提案されたアルゴリズム
6. 残された課題
7. 最後に

 

サンタクロース問題について

サンタクロース問題は公平分割問題の1種です。

身近な例だと、家族でお寿司の出前をとった時がこれに該当します。

問題設定

子供がn人、プレゼントがm個あり(n<<mとします）

子供iにとってのプレゼントj の幸福度がv_ijのとき

最も幸せでない子供の幸福度を最大にするように

各子供に（ひとつとは限らない）プレゼントを配る問題です。

ただし各プレゼントはいずれかの子供に分割せずに配らなくてはなりません。

具体例

ここで、子供が3人(n=3)、プレゼントが4個(m=4)の場合を考えます。

各マスに対応しているのは、その子供がプレゼントを受け取った時の幸福度を示しています。

例えば、青い服を着た男のが車のプレゼントだけを受け取ったら幸福度は0.5になります。

案1

青い服の男の子にサッカーボール、ピンクの服の女の子に車のプレゼント、赤い服の男に積み木とぬいぐるみをプレゼントする。

この場合、子供たちの幸福度は以下の通りとなります。

青い服の男の子: 0.3、赤い服の女の子: 0.1、赤い服の男の子: 0.7

これだと、赤い服の女の子がちょっと可愛そうですよね(画像はとても喜んでいますが)

案2

青い服の男の子に車のプレゼントと積み木、ピンクの服の女の子にぬいぐるみ、赤い服の男の子にサッカーボールをプレゼントする。

この場合、子供たちの幸福度は以下の通りとなります。

青い服の男の子: 0.6、赤い服の女の子: 0.7、赤い服の男の子: 0.6 この場合だと、案1よりもみんな幸福で、いいプレゼントの配り方をしたと思いますよね。

最小幸福度は0.6ですもんね(案1では最小幸福度は0.1だった)

このように「最小幸福度の最大化」がサンタクロース問題の目的です。

 

オフラインからオンラインのストーリー

今回紹介するのは「オンラインサンタクロース問題」です。

ここで、オンラインサンタクロース問題をイメージするためにこんなストーリーを考えてみました。

サンタクロースはn人の子供達にm個のプレゼントを毎年配ります。

昨年までは、 広いオフィスにm個のプレゼントを配置してから、 n人の子供達へのプレゼ?ントの配布を計算してから それぞれの子供向けにプレゼントを一気に送付しました。

子供が受け取るプレゼントは１つとは限りません。

1番幸福度が少ない子供の幸福度を最大にするように配布したいです！

新しいオフィスはとても小さく、プレゼントが1個到着するたびに 宅配便をつかって子供にそのプレゼントを送付します。

そうしないとオフィスには次のプレゼントを置くスペースがないのです！

サンタクロースは 広いオフィスを利用していたときと同じくらいに 子供たちを幸福度にできるのでしょうか?

1番幸福度が少ない子供の幸福度を最大にできるでしょうか？

 

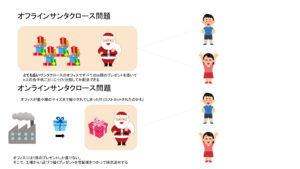
オンラインサンタクロース問題

ここではオンラインサンタクロース問題がどのように幸福度が計算されるか具体例を用いて説明します。

まず、工場から車のプレゼントが届きました。

サンタクロースは車のプレゼントをもらったら子供達がどれくらい幸福かは知っていますが、

次に積み木が来ることを知りません。

この時に、どういう判断をしたらいいのかを考えるのがオンラインサンタクロース問題です。

ここでは、青い服を着た男のが車のプレゼントを届けることにします。

次に工場から積み木がサンタクロースの元に届きました。

サンタクロースは積み木をもらったら子供達がどれくらい幸福かという情報と各子供たちの現在の幸福度を知っています。

これらの情報を元に、サンタクロースは積み木をどの子供にプレゼントするかを決めなければなりません。

こうして、全てのプレゼントを順番に配り切った後に、「最小幸福度の最大化」をしたいのがオンラインサンタクロース問題です。

 

オンライン問題の入力のモデル

今回は入力モデル(今回の場合、プレゼントがサンタクロースのところに届く順番)は２つあります。

1. Adversarial 入力モデル : 1番意地悪な入力を仮定し、このときのオンラインアルゴリズムの解などを評価します。
   

   Definition 1.1 (Adversarial Input). An adversary selects the value vector v ∈ [0, 1]^{n} of each arriving item for all the agents, as well as the order in which these vectors arrive.

2. Random-Order 入力モデル: ランダムな入力を仮定し、このときのオンラインアルゴリズムの解などを評価します。
   

   Definition 1.2 (Random-Order Input). An adversary selects the value vector v ∈ [0, 1]^{n} of each arriving item for all the agents, but these vectors are randomly permuted to determine their arrival order

補足: 投稿時点でTexで記述できる機能がないので、数式はご容赦ください

 

オンラインアルゴリズムの評価

オンラインアルゴリズムはCompetitive Ratioで評価します。

これは、オンラインアルゴリズムの解とオフラインアルゴリズムの解の比です。

オンラインアルゴリズムの解がオフラインアルゴリムの解よりも良くなることはないので

この比が、小さいほど、１に近いほどよいオンラインアルゴリズムになります。(最大化問題の場合です)

数式で定義すると以下の通りとなります。

ALG ≥ c · OPT − b ALG: オンラインアルゴリズムで得られた解

OPT: オフラインアルゴリズムで得られた最適解

c: Comeptitive Ratio b: Additive Regret 補足

• c (Comeptitive Ratio)=1, b(Additive Regret) =0のとき、オフラインと全く同じ結果が得られるのでこれが最高の結果となります
• また、OPTが十分に大きい場合、c (Comeptitive Ratio)の方が定数倍として効いてくるのでcが1に近ければ近いほど嬉しいです。 ここで、論文のTable1を見てみましょう。

各入力の仮定に対して、それぞれのComeptitive Ratioを示しているのがこの論文の成果の1つです。

(1-ε)は1に非常に近いのでとてもすごい結果です。

 

研究の成果

この研究の成果は3つあります。

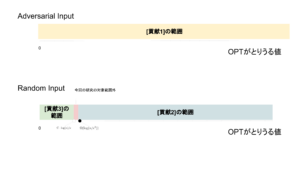
[成果1]

Adversarial 入力モデルでは

Comeptitive Ratioが1/nを超えるアルゴリズムはないと証明

Theorem 1.3 (Adversarial Input). In the adversarial setting, no algorithm can obtain a competitive ratio better than 1/n

 

[成果2]

Random-Order 入力モデルでは

OPT≧Ω(log(n/ε^2)) の時

任意のε>0に対して Comeptitive Ratioが(1-ε)となるOnline Fractional Algorithmがある

->ほとんどの場合は、よいオンラインアルゴリズムがある! (オフラインの結果とほぼ変わらない解が計算できる)

*OPTはオフラインのときの最適解

Theorem 1.4 (Random Order: Algorithm). For any ε > 0, there is an online fractional algorithm for the Santa Claus problem that has a competitive ratio of (1 − ε) in the random order input model under the assumption that OPT ≥ Ω (log n/ε2) [成果3]

Random-Order 入力モデルでは

OPT<C・log(n)/εの時 Comeptitive Ratioが(1-ε)となるオンラインアルゴリズムはない

*OPTはオフラインのときの最適解

Theorem 1.5 (Random Order: Impossibility Result). For any ε ∈ (0, 1), there is no online algorithm for the Santa Claus problem in the random order input model that has a competitive ratio of (1 − ε) when OPT < C ·log (n) /ε for some (absolute) constant C > 0

 

実際に提案されたアルゴリズム

基本的な考えはとてもシンプルです。

m/2(プレゼントの半分までは)到着したアイテムを最も満足度の低い子供に割り当てることである プレゼントを半分配り終わったら、今までのことは忘れてもう1度同じ配布方法を行う ここで注目してもらいたいのは、2点です。

• 前半、後半の戦略は φ: the smoothed minimum functionに入れた関数に対して、Greedyな方法になっている
• 前半と後半が依存していない 以上を踏まえてこの論文のすごい部分を話ていきたいと思います。

すごいPoint: Greedyな方法だが、全体を上手に考慮したようなアルゴリズムになっている

論文のLemma 2.3.より φ: the smoothed minimum functionは以下の性質を持っています。

ここで言いたいのは 本当に最小化したいのは右側のmin(ui)なんだけど、 φ(u)を用いてることによってかなりいい近似ができているということです。

この性質により、今までの幸福度が1番小さい子の幸福度の子が大きくなるようにプレゼントの割り当てができるようになります。

このthe smoothed minimum functionが最小幸福な子供に反応するようにうまく設計されているのがすごいところです。

すごいPoint: 前半と後半に分ける

Greedyな方法は今まで結果に強く依存します。しかし、この論文はその依存はn/2 – 1 個前までした依存しないことを示しています。

確かに論文の数式を追っていくと言っていることはわかるのですが、その凄さはまだ検討中です。(かなりすごいことをしていると思います)

The benefit of this restart will yield a tolerable error as compared to the optimal offline solution in each half of the allocation procedure, rather than a continuously accumulating divergence between the two solutions: each arriving job’s allocation is only dependent upon (at most) n/2 − 1 other decisions. We leverage this randomness to obtain the final competitive guarantees [52].

 

残された課題

今回の研究ではOPT(オフラインの解)によって、実はオンラインアルゴリムの解析ができていない範囲があります。それは貢献2と貢献3の間です。

しかし、その部分は非常に小さいです。著者たちはOpen Problemだと言っています。

 

最後に

サンタクロース問題の意義を自分なりに記述したいと思います。

自分がサンタクロースになった気分で考えてください。

もっといい問題設定があるんじゃないか?と思った方もいると思います。

例えば、「子供達の幸福度の総和を最大化」というのも自然な問題です。

しかしこの場合、少数の子供が莫大な幸福度を得て、他の多くの子供達がほんのわずかな幸福度しか得られない以下のようなプレゼントの分配が最適解になる可能性があります。

赤い服の男の子と他の子供達との差がすごいですね…

まさに、格差社会！って感じです。

今回の、幸福度が最小の子供の幸福度が最大になるようにプレゼントを分配することは、より格差のすくないFairな分割になることが期待できるのです。

サンタさんがどちらを望んでいるのかはおわかりですね！

それでは、皆さん、Merry Christmas! (´･ω･)ﾉｼ

Reference

[1] MohammadTaghi Hajiaghayi, Mohammad Reza Khani, Debmalya Panigrahi, Max Springer: Online Algorithms for the Santa Claus Problem. CoRR abs/2210.07333 (2022)

NeurIPS 2022(採録)