はじめに
2023年12月より協業リテールメディアdiv.にてインターンシップをしています。早稲田大学大学院1年の澤木陽人です。大学院ではパターン認識や機械学習を専攻しており、今回のインターンでもML/DS職として参加しました。
本記事では、配属部署の取り組みと、私が実際に取り組んだ効果検証手法について紹介します。
アプリ運用カンパニーの取り組み
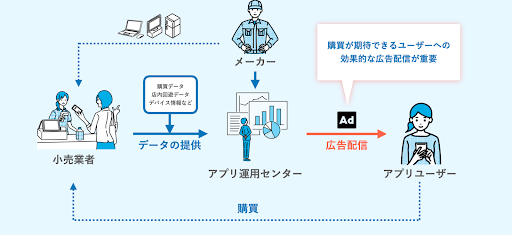
インターンで配属されたのは、協業リテールメディアdiv.の中のアプリ運用カンパニーという部署のチームでした。アプリ運用カンパニーの役割は、大まかに言えば「小売業とタッグを組みながら効率的に広告配信を行うためのブレインとなる部署」です。
小売店舗では様々なメーカーが作った商品が販売されているため、当然メーカーは「自社の製品がよく売れて欲しい」と考えています。
ここで、小売業とサイバーエージェントが協力して作られた販売促進のためのデータ基盤が役に立ちます。これは、このデータ基盤が、購買データやサイネージ、連携アプリのログなどを活用することで、顧客の属性・興味関心に基づいた消費者ニーズを捉え、戦略的にマーケティングを行えるためです。
これにより、「広告予算を効率よく使って、効果的に広告を配信したい」というメーカーの声に応えることが可能なのです。
より多くのメーカーにこの仕組みを使いたいと思ってもらえるよう、データサイエンスや機械学習などの先進技術を駆使して価値ある商材を開発・運用していくことが、アプリ運用カンパニーの役割であると言えます。
キャンペーンの効果検証
実際に配信された広告がどの程度効果があったかは、次の意思決定や課題発見に大きな示唆を与えてくれるため、アプリ運用カンパニーのチームにとっても大きな関心があります。
どのキャンペーンでどれほどの広告効果が出ていたのか、どのような特性を持つ人に効果が現れやすいのか、これらを検証しモニタリングすることができれば、チームの意思決定が円滑になるだけでなく、現在提供しているサービスの有用性を裏付け、より大きな価値を主張することができます。
そのためには、蓄積されたたくさんのデータからより良い分析を通じて、効果を推定する枠組みが不可欠です。
ここからは、基本的な効果検証の方法論について説明したのちに、今回私が実際に携わった分析の概要、課題点を説明し、それを踏まえて改善手法の説明を行います。
効果検証の基本
通常、効果検証の手続きでは、何かしらの介入があった場合となかった場合に、効果を測定したい指標(処置効果)にどれだけの差が生じるかを推定します。今回ここでいう介入とは広告の配信にあたり、測定指標はキャンペーン期間中の購買にあたります。つまり、広告が配信された場合とされなかった場合で、購買率がどれだけ上昇しているかを処置効果として観測したいということになります。
しかし、同じユーザーに対して「広告を配信した」「広告を配信しなかった」という2通りの世界線をどちらも経験させることはできませんから、真の処置効果というものを知ることは不可能です。そこで、通常は介入があったユーザーグループ(処置群)と、介入のなかったユーザーグループ(対照群)を比較することによって、処置効果を推定します。
ある期間中に購買があったかどうかをY(購買したなら1・しなかったら0のカテゴリ変数)、そのユーザーが属するグループをT(処置群を1・対照群を0とするカテゴリ変数)とすれば、それぞれのユーザーグループに対してYの平均を計算し差を取ることで、購買率の差が求まることになり、処置効果として推定できます。すなわち
処置効果 = $$E\Bigr[Y^{(T=1)}-Y^{(T=0)} \Bigr] =E[Y|T=1]– E[Y|T=0]$$
と書くことができます。これは\(T\)が与えられた場合の条件付き平均の差に相当するので、
次の線形回帰における\(T\)の係数 $$\beta_1$$ に一致します。
$$Y = \beta_0 + \beta_1 T$$
これが最も基本的な広告効果の推定方法となります。
分析の概要と課題点
今回は、配属部署が提供しているAIセグメントというサービスに関連して分析を行いました。AIセグメントとは、過去の購買履歴などに基づき、商品カテゴリごとの購買の見込み(以下、カテゴリ予測値)をユーザーごとに予測し数値として割り振ることで、購買可能性の高いユーザーを選定するAI活用の仕組みです。カテゴリ予測値に閾値を設け、一定の値以上だったユーザーに広告を配信することで、広告予算を効果的に運用することができます。
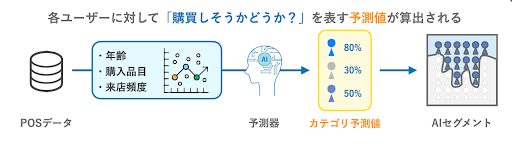
徐々にAIセグメントを活用したキャンペーンは増えており、カテゴリ予測値が高かったユーザーほど購買に結びつきやすいという結果が出ている一方、「カテゴリ予測値が高いこと」と「広告配信による効果が出やすいこと」の関連性はまだしっかり検証されていない状況にありました。
そこで、「カテゴリ予測値の高低が、広告効果に違いを及ぼしているか?」を検証することが今回の分析の目標となりました。
これをナイーブに比較するのであれば、先ほど述べた方法で簡単に検証が可能です。
- カテゴリ予測値を特定の間隔で刻み、複数のグループ(Bin)に分ける
- 各Binのユーザーのデータを使って効果検証する
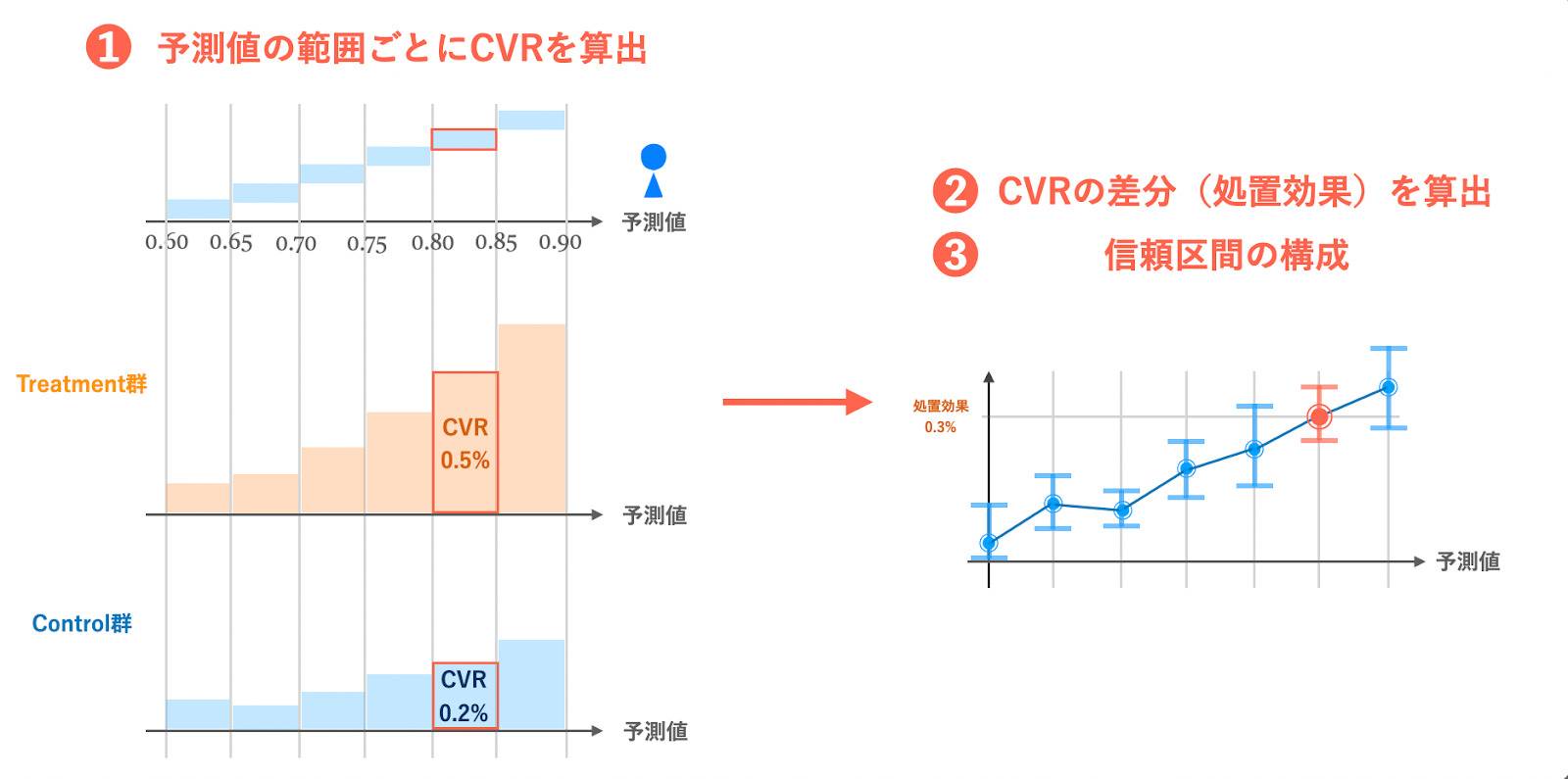
実際私もデータをいただいてすぐにこれを試しましたが、分析結果を見ると、カテゴリ予測値が大きな領域ではスムーズな結果が結果が得られず、回帰が不安定になっている様子が見受けられました。
この原因として考えられるのは、実際に対象商品を購買をするユーザーが少ないことにより、「大きなカテゴリ予測値が割り振られるユーザーが少ないこと」です。
キャンペーン期間中に対象商品を買う人はユーザー全体に対して見ればかなり少ないため、カテゴリ予測値(=購買見込み)が高い値を示す人は多くはありません。高い予測値の領域では、割り振られるユーザーの数が急激に減少してしまうのです。
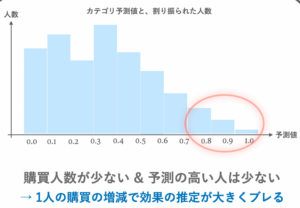
その結果として次のような悪影響が出てきます。
- ユーザー数が少ない領域ではたった1人の購買がCVRに大きな影響を及ぼし、効果の推定が難しい
- ユーザー数を確保するためにBinを広く取ると、大雑把な考察しか得られない
このような「回帰の安定性と分析のきめ細やかさのトレードオフ」の課題を解決するためには、少数ユーザー領域において、より安定した効果検証が行える枠組みを取り入れる必要がありました。
提案手法
上記の問題に対する取り組みとして、主に次の2つの仕組みを効果検証の手続きに取り入れました。
- データ数に応じてBinの幅が増減する、可変長Binの導入
- 処置効果の推定に重み付き局所回帰(Weighted Local OLS)モデルを導入
アルゴリズム全体としては次のようになります。
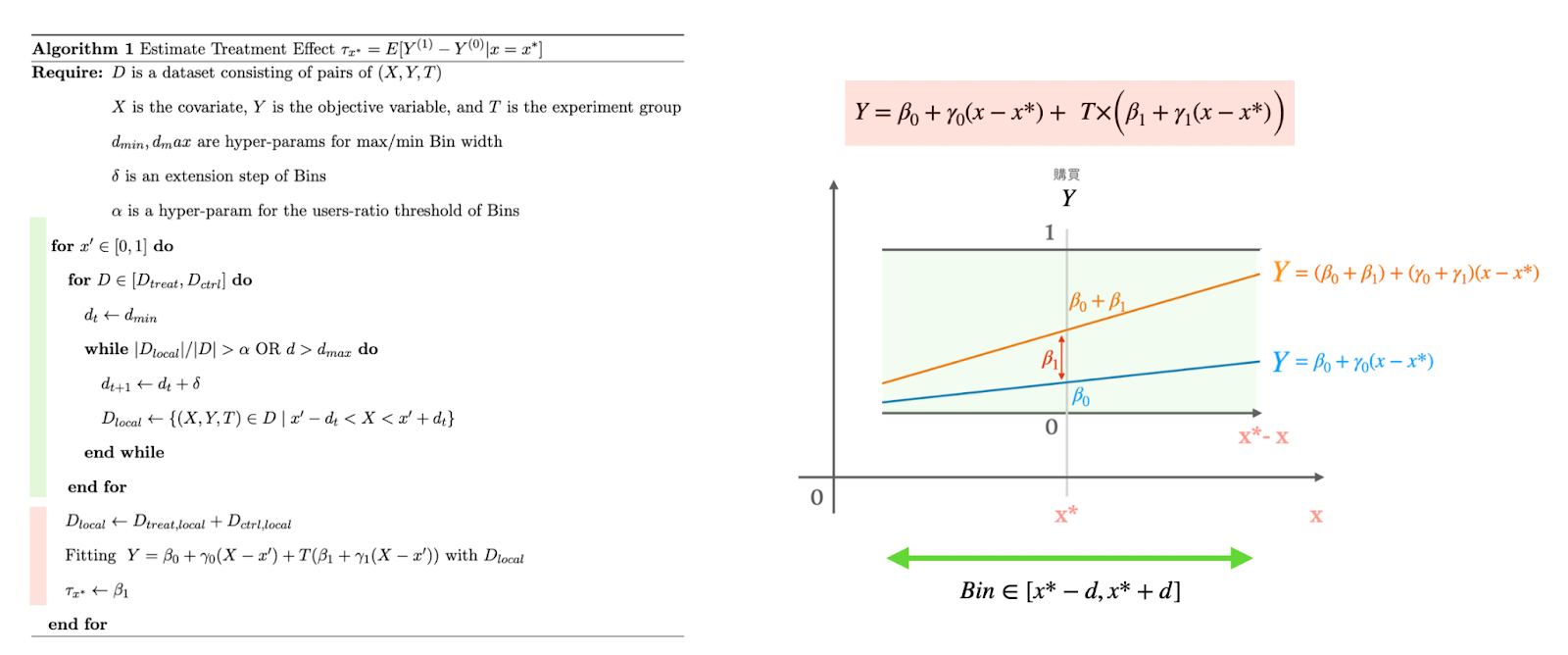
それぞれの目的と手法について説明します。
1. 可変長Binの導入
基本的な方法で触れた通り、最もナイーブな方法は、カテゴリ予測値を一定の幅で切ることでBinを構成して検証することでした。しかし、これでは人数が十分でないBinでは予測が不安定化したり、統計的な有意性が見出しにくいなどの問題がありました。そこで、「処置群と対照群のそれぞれのBinにおいて、割り振られるユーザー数が群全体の一定の割合を超過するまで拡張する」という処理を行うことで、本来ユーザーが少ない領域でも安定した回帰が行えるようになります。
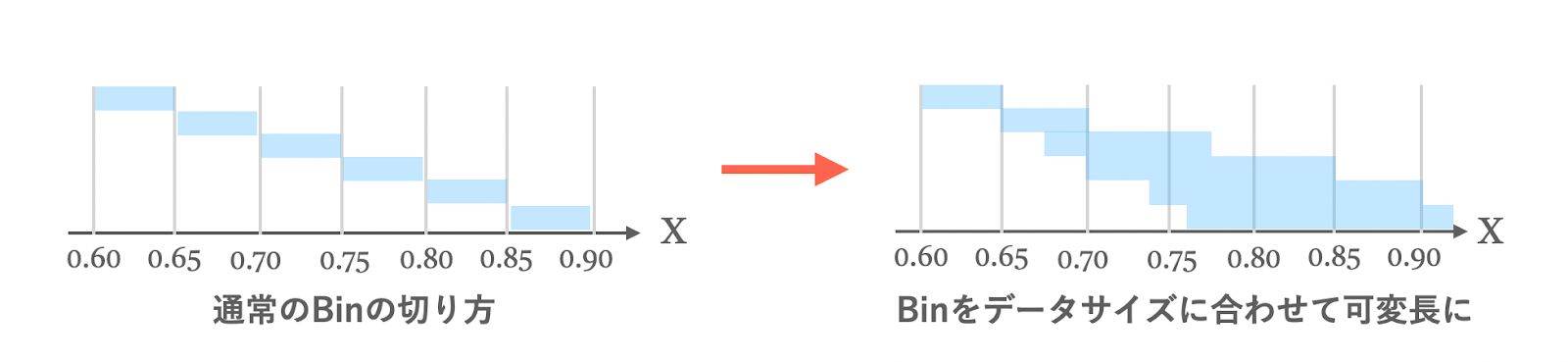
Binを可変長にすることで、それぞれの分析の対象となるユーザーを一定数確できるようになりますが、これにはデメリットもあります。これも上述した通り、Binが広くなったことにより得られる結果が大雑把になってしまうのです。あるカテゴリ予測値におけるピンポイントな処置効果を調べたいのに、その前後の大きな範囲をまとめて分析しては、データのディテールが失われてしまいかねません。それを防止するのが次の仕組みです。
2. 処置効果の推定に局所回帰モデルを導入
可変長Binの弱点を補うため、回帰式に工夫を施します。
変数に処置Tのみを含めた回帰で推定される処置効果は、両ユーザーグループのCVR差を計算するのと全く等価なため、Binが広いとユーザーが密集しているカテゴリ予測値周辺の影響が色濃く出てしまい、本当に知りたいカテゴリ予測値における処置効果が推定できない可能性があります。
そこで、
- Binの中でさらに変動を捉えられるようにする → 局所回帰
- 処置効果を推定したい点から離れるほど回帰の影響を小さくする → 重み付き回帰
という二つのアプローチを統合し、効果検証の枠組みに導入します。
結論からいうと、回帰式と損失関数を次のように変更しました。
$$Y=\beta_0+\gamma_0(x-x^*)\ +\ T\times\Bigr(\beta_1+\gamma_1(x-x^*)\Bigr)$$
$$\text{loss} = \sum_{i=1}^{n} k(x,x^*)(y_i – \hat{y}_i)^2$$
ここで\(x\)は各データのカテゴリ予測値、\(x^*\)はBinの中心となるカテゴリ予測値で、損失項の\(k(x,x^*)\)はガウスカーネルです。この回帰式では、\(\beta_1\)の値が推定された処置効果となります。
回帰式を見ると
$$\beta+\gamma(x-x^*)$$
という一次式が新たに組み込まれていることがわかります。
これは、Binの中に含まれたデータをさらにBinの中心値の周りで線形回帰しているためです。これにより、Binに含まれたユーザーのカテゴリ予測値の偏りによって生じるバイアスを大幅に低減でき、処置効果を知りたいカテゴリ予測値 $$x=x^*$$ でのピンポイントな推定が可能になります。
また、ガウスカーネルによる損失の重み付けによって、データがBinの中心から離れるにつれて回帰に及ぼす影響が小さくなり、これもバイアスが大きくなりすぎることを防ぐ役割をします。
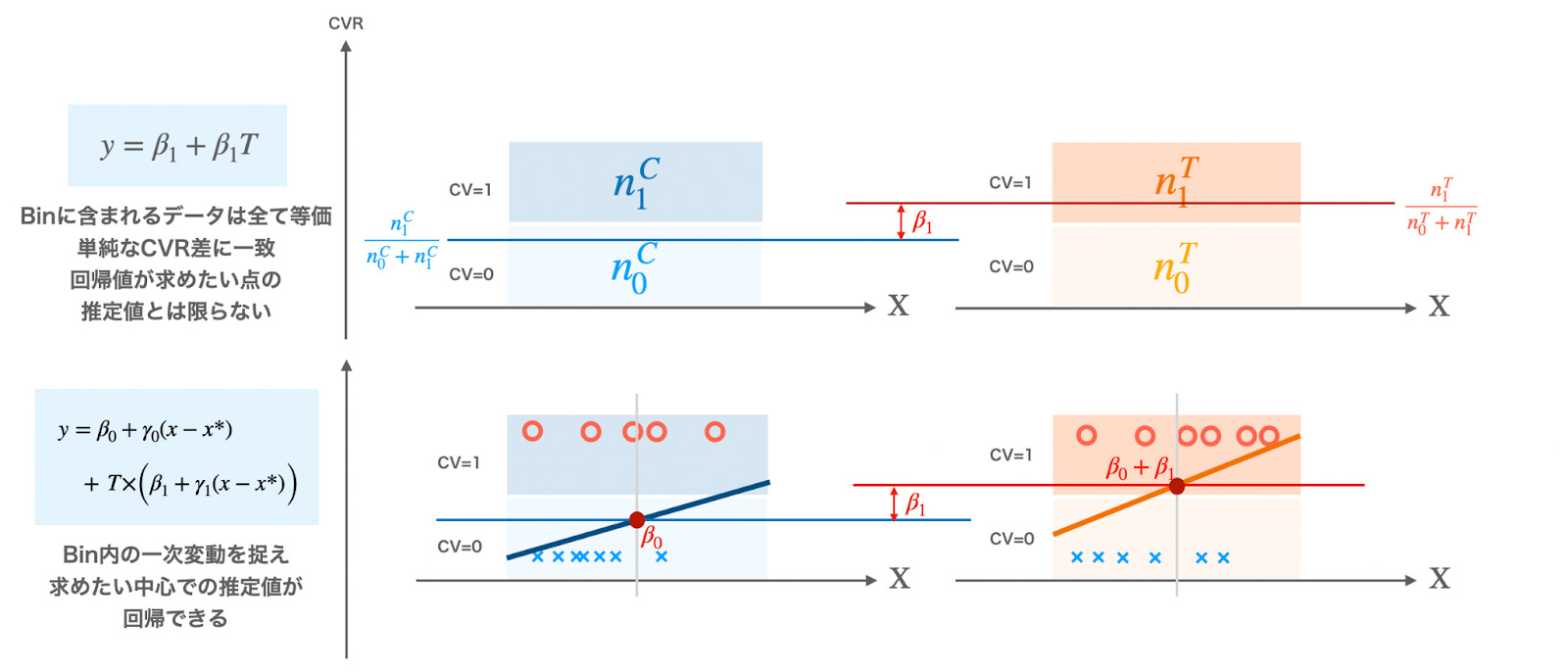
トイデータによる結果
実際のキャンペーンの効果はここでは載せることができないため、semi-syntheticなトイデータの分析結果で、効果を実感していただけたらと思います。
以下のトイデータは、実際にAIセグメントに用いられたユーザーごとのカテゴリ予測値を用いて、「カテゴリ予測値*0.1」の確率で購買を割り振った反合成データです。実際のデータでは真の処置効果は測定ができませんが、このデータでは正解の処置効果を決めて作成しているため、どれだけ正しく推定できたかを検証可能です。
結果を見てみると、ユーザーが少ない高予測値領域においても比較的頑健に推定が行えており、信頼区間も非常に小さくなっていることがわかります。
信頼区間が小さくなることで処置効果があった際に統計的な有意性を主張しやすくなるため、広告効果をよりよく把握することができるようになります。
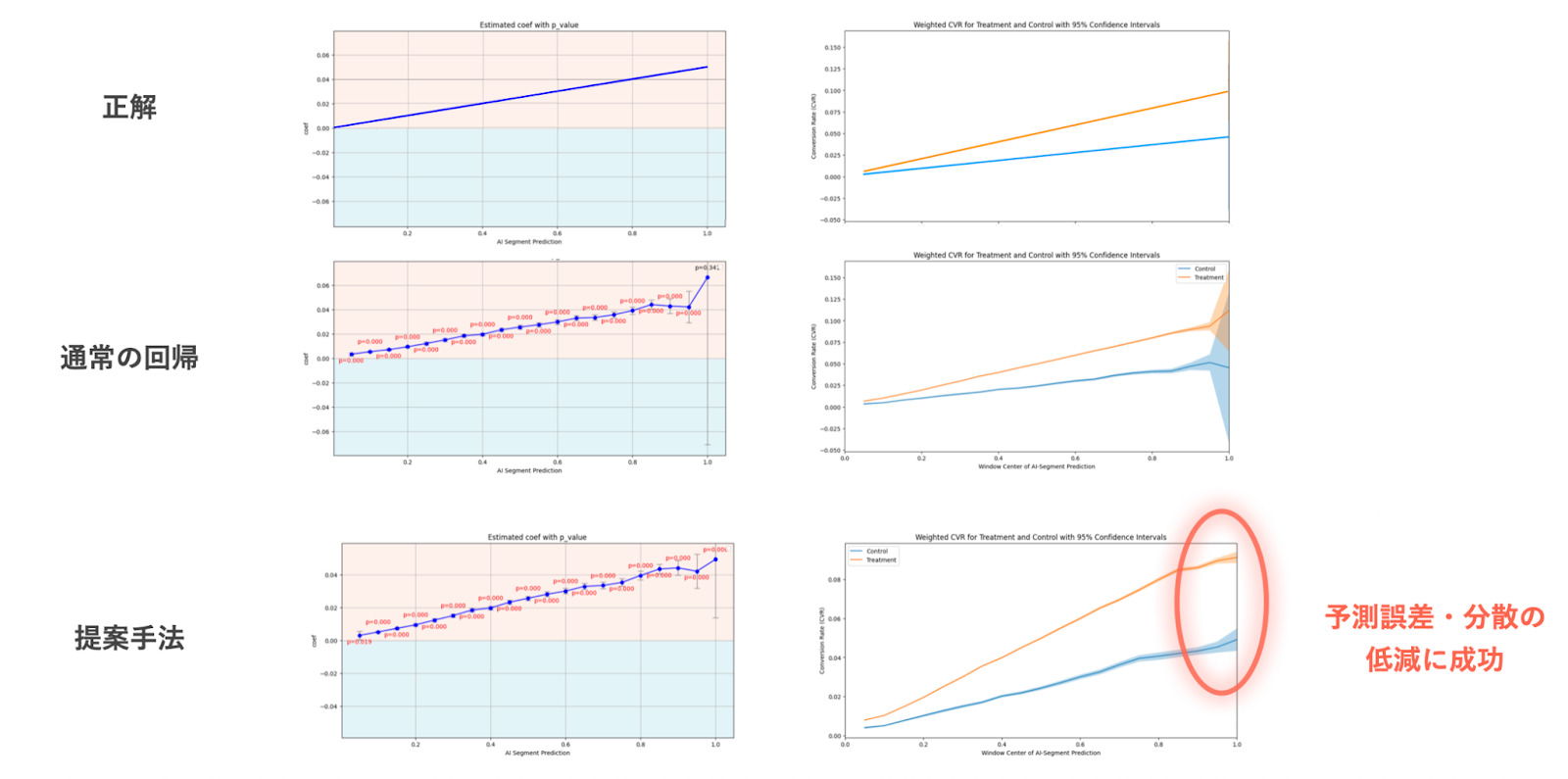
おわりに
単なる分析に終わらず、チーム全体がより確度の高い意思決定を行うために正しく情報を解釈できる枠組みを作ることの価値を感じたインターンシップでした。分析にあたっては、チームのDSメンバーの皆様だけでなく、毎週AI Labの方々からも多大なフィードバックをいただき、多方面からのサポートを受けながら取り組めたことを大変ありがたく思っています。
技術面、知識面で至らぬところも多くあった中、たくさんの支えのおかげで、自身にとっても非常に有意義なインターンシップとすることができました。トレーナーの河野さん、メンターの青見さん、早川さん、須ヶ﨑さんを初め、AI Labの岡さん、安井さん、チームの皆々様、本当にありがとうございました。

