形式手法入門：生成 AI 時代の『設計』のあり方について

はじめに

こんにちは、2025 年新卒で ABEMA の広告配信システム開発チームに所属している戸田朋花です。

生成 AI を活用した開発が広がる中で、コードを書くこと自体のハードルは大きく下がりました。
一方で、生成 AI に「どのようなシステムを実装して欲しいのか」を正確に伝える難しさを日々感じています。

2 週間ほど前には spec-driven development を掲げた AI 統合開発環境の Kiro が AWS からリリースされ、話題となりました。
Kiro ではユーザーとの対話を通じて Requirements, Design, Task list を順に作成することで、まずシステムの設計を明確にしてからコーディングに入るプロセスが取られています。この方法は冒頭で述べた課題に対する 1 つのアプローチになるでしょう。しかし、依然として生成 AI と自然言語で設計の微妙な調整を行うことが求められています。

このような背景から、今後のソフトウェア開発において「設計そのものをどのように記述するのか」がますます重要になっていくと考えています。

本記事では設計を正確に記述し検証することができる「形式手法」の入門的な内容についてご紹介します。

形式手法に着目した背景

皆さんはシステムの設計をどのように書いていますか？
業界によっても異なると思いますが PowerPoint や Excel, Markdown, Mermaid などで書くことが多いのではないでしょうか。
設計には標準的な書き方は存在せず、自然言語や図で書かれることがほとんどです。そのため曖昧さが生じてしまいます。
この曖昧さは仕様ミスや誤解を招き、最悪の場合システムの障害や脆弱性を発生させてしまいます。

設計の時点で曖昧さが排除されていて正しさをある程度保証できれば、最小限の手戻りで効率的に開発を進めることができ、運用中の障害も最小限に減らせるのではないかと考えています。

曖昧さのない設計は生成 AI との協働においても重要だと考えています。
生成 AI は自然言語でやりとりできることが強みですが、曖昧な自然言語で意思疎通をするのは難しいこともあります。
例えば、ある実装について生成 AI と相談する時、自然言語を使って説明するよりもソースコードを貼った方が簡単かつ正確に生成 AI とやりとりすることができます。
設計についても同様で、曖昧さのない共通言語があった方がより効率的に生成 AI と対話できるのではないでしょうか。
また、曖昧さのない設計は生成 AI によるコード生成においてガードレールとしても機能します。
このような背景から、私は形式手法に着目しました。

また、この課題感をもとに IPA の未踏 IT 人材発掘・育成事業で開発しているソフトウェアについても最後にご紹介しているので、興味のある方はぜひ読んでもらえると嬉しいです！

形式手法とは

形式手法とは、システムの設計・振る舞いを形式的な言語で記述し、その正しさを検証する手法です。
形式的な言語とは、厳密に決められた記号・構文を持ち、曖昧さのない言語のことです。

形式手法におけるシステムの正しさを検証する方法として、定理証明とモデル検査の二つが代表的です。

定理証明は、一連の要件から特定の結論が論理的に導かれることを証明するアプローチです。
システムを一連の論理式 \(\Gamma\) として記述し、システムが満たすべき性質はまた別の論理式の集合 \(\phi\) で表します。
\(\Gamma\) から \(\phi\) を導出するような証明を見つけることで、システムの正しさを検証します。

モデル検査は、特定のシステムのモデルが与えられた仕様を満たすことを計算によって決定するアプローチです。
本記事ではモデル検査について解説します。

モデル検査とは

モデル検査とは、システムの要件に合うモデル M と、システムが満たすべき性質を表す論理式 φ について \(M \models \phi\) が成り立つかどうかを決定することです。
\(\models\) は二重ターンスタイル記号というもので、ここではモデル M が論理式 φ を満たすということを表しています。

モデル検査は、主にリアクティブシステムと呼ばれるシステムを対象とします。
リアクティブシステムとは、環境に反応し、終了することを意図しないシステムです。
私たちが普段開発している API サーバー等はリアクティブシステムです。
このリアクティブシステムを抽象化し、モデルとして扱うことで検査を行います。

システムのモデル検査をするために、遷移システムとしてモデリングします。
遷移システムについては、後で解説します。

システムが満たすべき性質を表す際に代表的に使われるのが時相論理です。
時相論理は、命題が時間の流れに沿ってどのように成り立つかを記述するための論理体系です。
例えば、結果整合性は「いつか」データが収束することを表しています。
この「いつか」という表現は将来のある時点で性質が成り立つことを示しており、このような性質は時相論理を用いて表現することができます。

時相論理にはさまざまな種類があり、この後で計算木論理 (CTL) と、線形時相論理 (LTL) について取り上げます。

時相論理を用いることで、システムの安全性 (Safety) や活性 (Liveness) を検査することもできます。
Safety とは「悪いことが絶対に起こらない」ということを表し、Liveness は「良いことが最終的に起こる」ということを表します。

遷移システムとは

モデル検査は、システムを遷移システムとしてモデリングします。
遷移システム \(M\) は状態集合 \(S\)、遷移関係 \(\rightarrow\)、ラベリング関数 \(L(S)\) から構成されています。

$$M=(S,\rightarrow,L)$$

遷移関係とはある状態 \(s\) から特定の状態 \(s’\) に遷移できるという関係のことです。
ラベリング関数 \(L(s)\) とは、ある状態 \(s\) で真となる命題の集合です。

話が抽象的で難しいので 2 フェーズコミット (2PC) を例に説明します。

2PC とは

2PC とは、分散システムにおいて、複数のノード間でトランザクションのコミットやアボートを決定するためのプロトコルです。
まず最初に、Coordinator が全ての Participant に prepare を送信します。

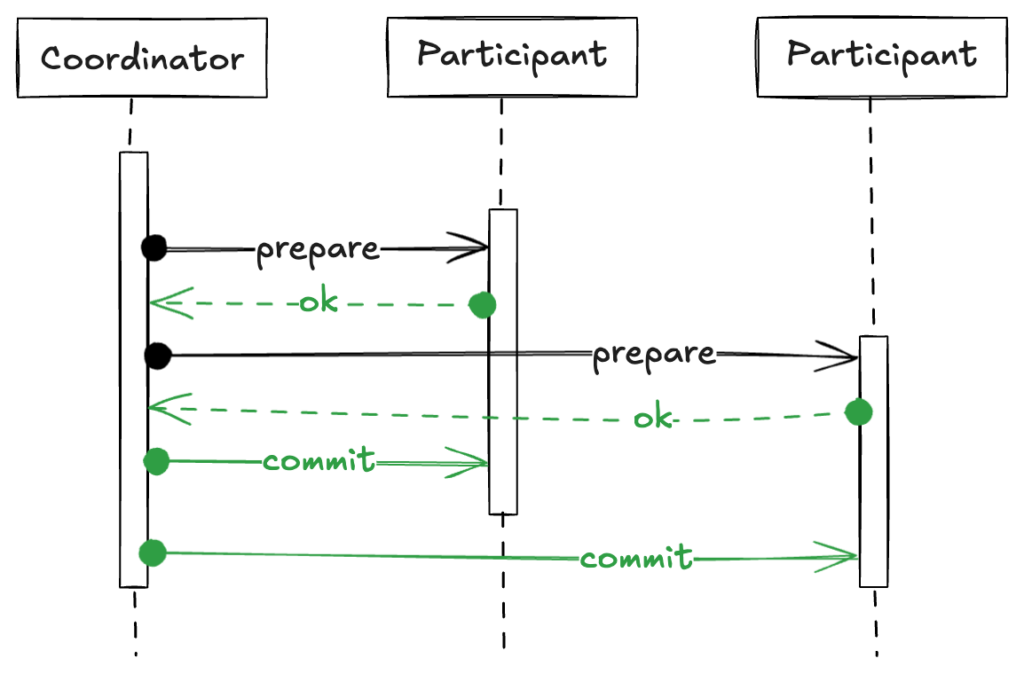
全ての Participant から正常な応答が返ってきた場合、Coordinator は commit を送信します。

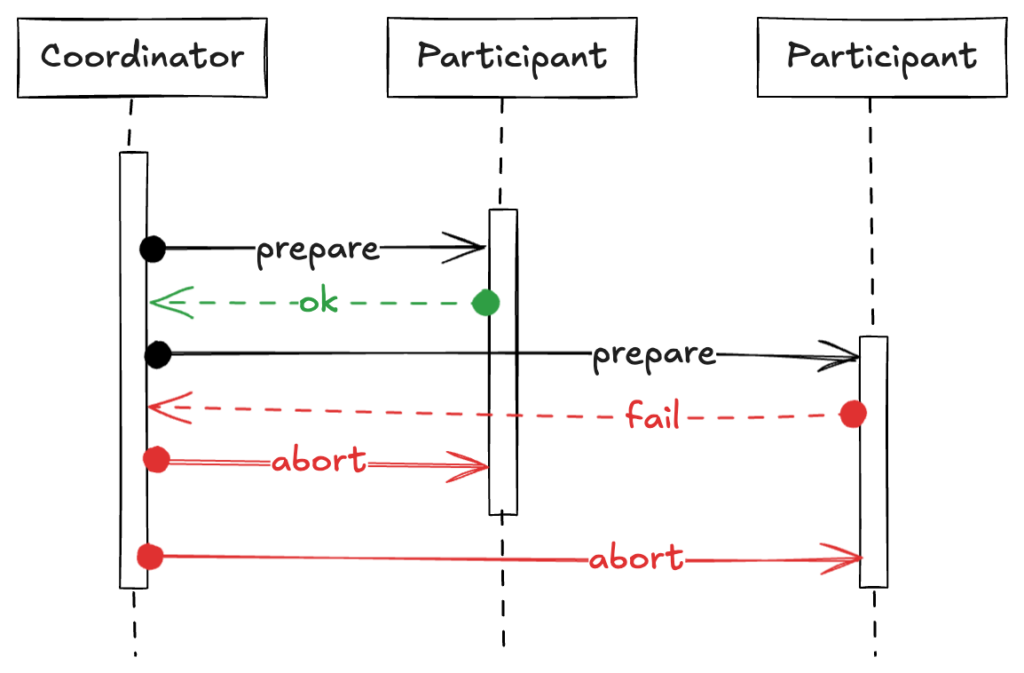
Participant のうちひとつでも異常な応答を返した場合は、Coordinator は abort を送信します。

2PC の遷移システム

2PC を遷移システムとしてモデリングすることを考えます。
上で述べたように、遷移システム \(M\) は状態集合 \(S\)、遷移関係 \(\rightarrow\)、ラベリング関数 \(L(S)\) から構成されています。これらを一つずつ考えていきます。

まずは状態集合 \(S\) から考えていきます。
2PC が取る状態は以下のように考えることができます。

• s0: Init
• s1: WaitingForVotes
• s2: AllYesReceived
• s3: SomeNoReceived
• s4: Commit
• s5: Abort

次に、遷移関係 \(\rightarrow\) について考えていきます。
まず Init からは WaitingForVotes に遷移可能なため、\(s_0 \rightarrow s_1\) があります。
また WaitingForVotes からは AllYesReceived または SomeNoReceived に遷移可能なため、\(s_1 \rightarrow s_2\)、\(s_1 \rightarrow s_3\) もあります。
AllYesReceived からは Commit に遷移可能なため、\(s_2 \rightarrow s_4\) があります。
SomeNoReceived からは Abort に遷移可能なため、\(s_3 \rightarrow s_5\) があります。

最後にラベリング関数 \(L(S)\) について考えていきます。
ラベリング関数とは、ある状態 \(s\) で真となる命題の集合のことでした。
各状態でどんな命題が真になるか考えてみます。
まず、\(s_0\) では特に満たす命題がないので \(L(s_0)=\emptyset\) となります。
次に、\(s_1\) では、「prepare を送信した」という命題を満たします。\(L(s_1)=\{PrepareSent\}\) と書くことにします。
\(s_2\) では、「全員が正常な応答を返した」という命題を満たします。これを \(L(s_2)=\{AllYes\}\) と書くことにします。
一方 \(s_3\) では、「少なくとも 1 つが異常な応答を返した」という命題を満たします。これを \(L(s_3)=\{SomeNo\}\) と書くことにします。
\(s_4\)、\(s_5\) ではそれぞれ「Commit した」「Abort した」という命題を満たします。これを \(L(s_4)=\{Commit\}\)、\(L(s_5)=\{Abort\}\) と書くことにします。

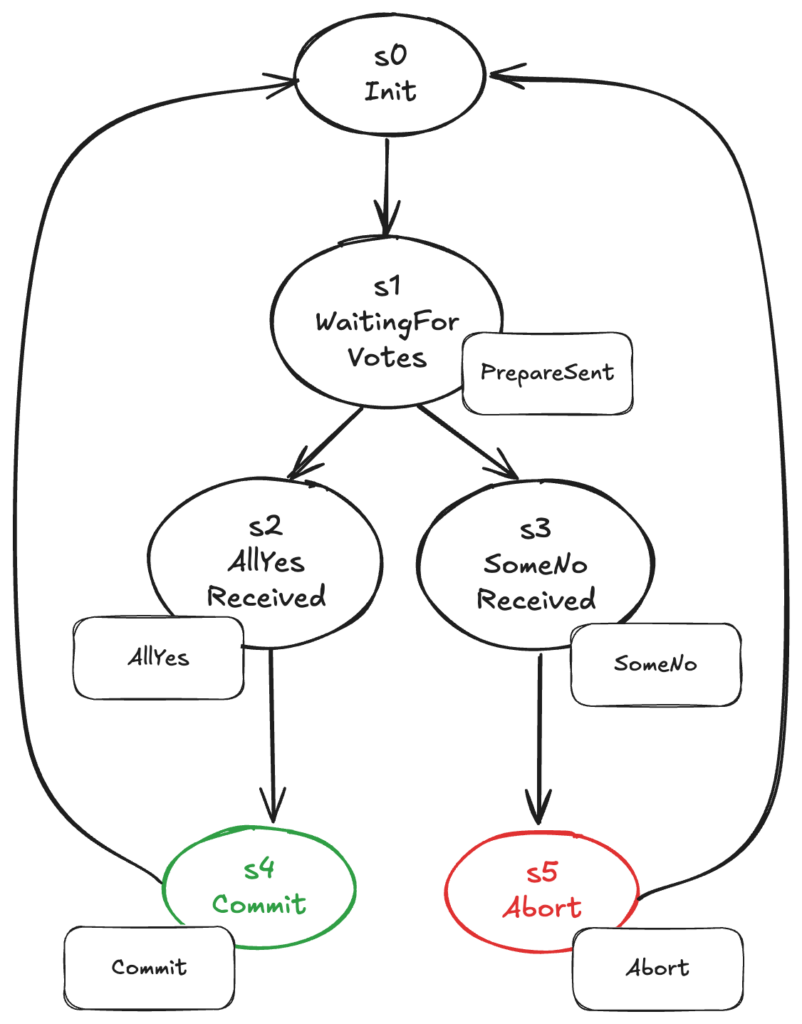
遷移システムに必要な要素が集まりました！
これを図示すると、以下のようになります。

線形時相論理 (LTL)

線形時相論理 (LTL) についてご紹介します。
線形時相論理では、未来を無限に伸びるパスとして定義します。
未来には複数の可能性があるため、LTL では複数の異なるパスを対象とします。

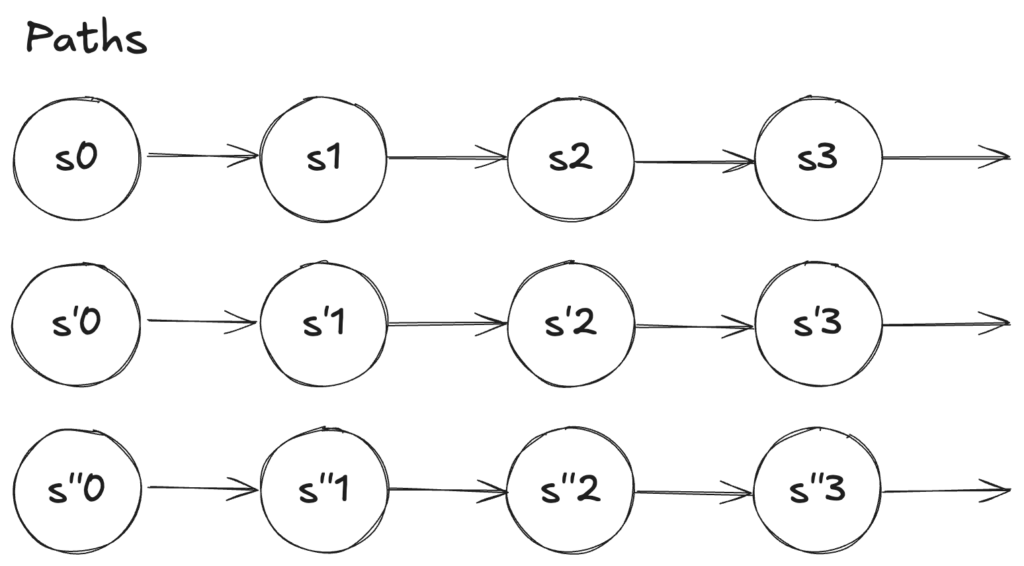
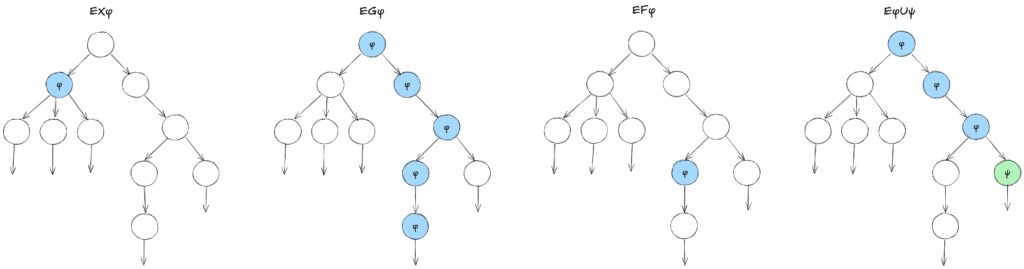
LTL の代表的な演算子として、\(X\)、\(F\)、\(G\)、\(U\)、\(R\) があります。
それぞれの演算子が何を意味するのかを、図解を交えつつ簡単に説明します。

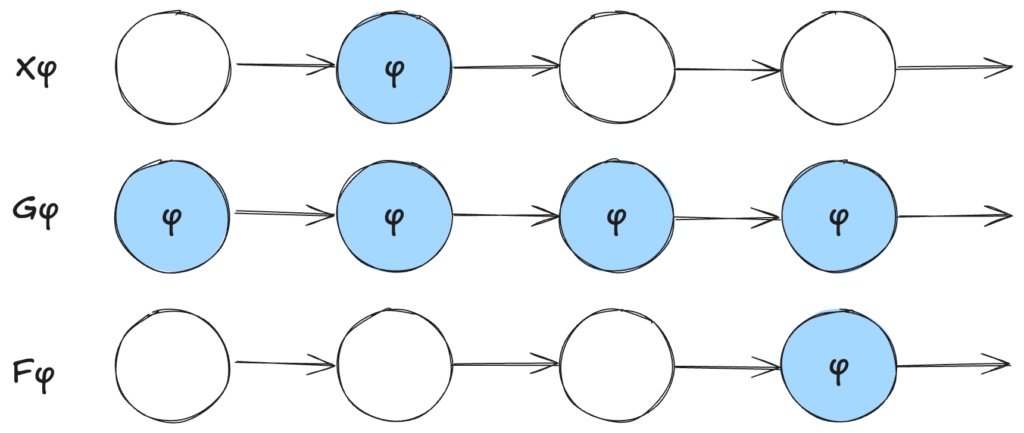
\(X\) は ‘neXt state’ のことで、次の状態を意味します。
\(G\) は ‘Globally’ のことで、全ての未来の状態を意味します。
\(F\) は ‘Future’ のことで、いくつかの未来の状態を意味します。

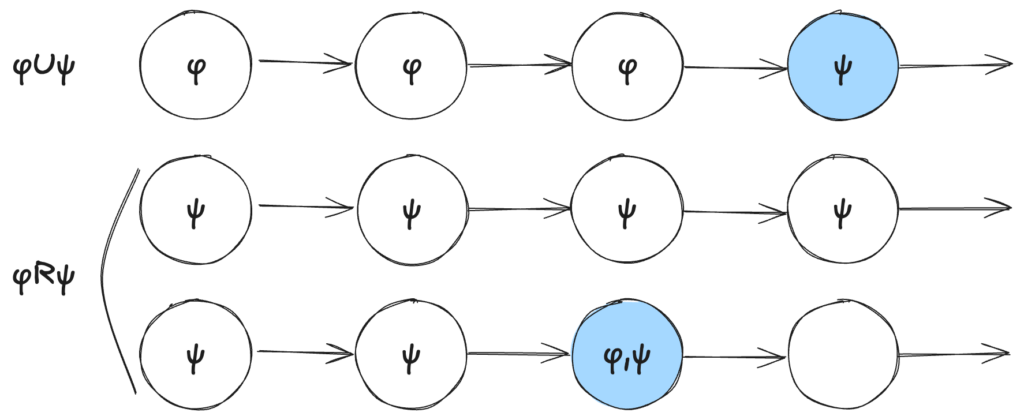
\(U\)、\(R\) は二項演算子です。
\(\phi U \psi\) は ‘Until’ のことで、\(\phi\) が \(\psi\) が成り立つまでの間成り立つことを示します。
\(\phi R \psi\) は ‘Release’ のことで、\(\psi\) が \(\phi\) が成り立つ瞬間まで継続して成り立つこと、または \(\psi\) が継続して成り立つことを示します。

2PC を用いた LTL の例

先ほどの 2PC の例で LTL で表現できる性質をいくつか挙げてみましょう。

「全ての Participant が正常な応答をした場合は、最終的に Commit される。」(Liveness)

$$G (AllYes \rightarrow F Commit)$$

「Prepare を送信したら最終的に Commit または Abort が起きる。」(Liveness)

$$G (PrepareSent \rightarrow F (Commit \vee Abort))$$

「Commit と Abort は同時に起きない。」(Safety)

$$G \neg(Commit \wedge Abort)$$

LTL はパスそのものの性質を記述することに優れており、以下のような記述が可能です。これは、この後説明する CTL で記述することは難しい内容になります。

「もし、ある実行経路で無限回 Prepare を送り続けるなら、その実行経路では無限回 Abort か Commit のいずれかが起きる。」

$$GF PrepareSent \rightarrow GF (Commit \vee Abort)$$

計算木論理（CTL）

LTL では時間を無限のパスとして表し、このパスについて評価すると述べました。
これに対して計算木論理（CTL）では時間を未来に向かって枝分かれしていく無限の木構造としてモデル化します。

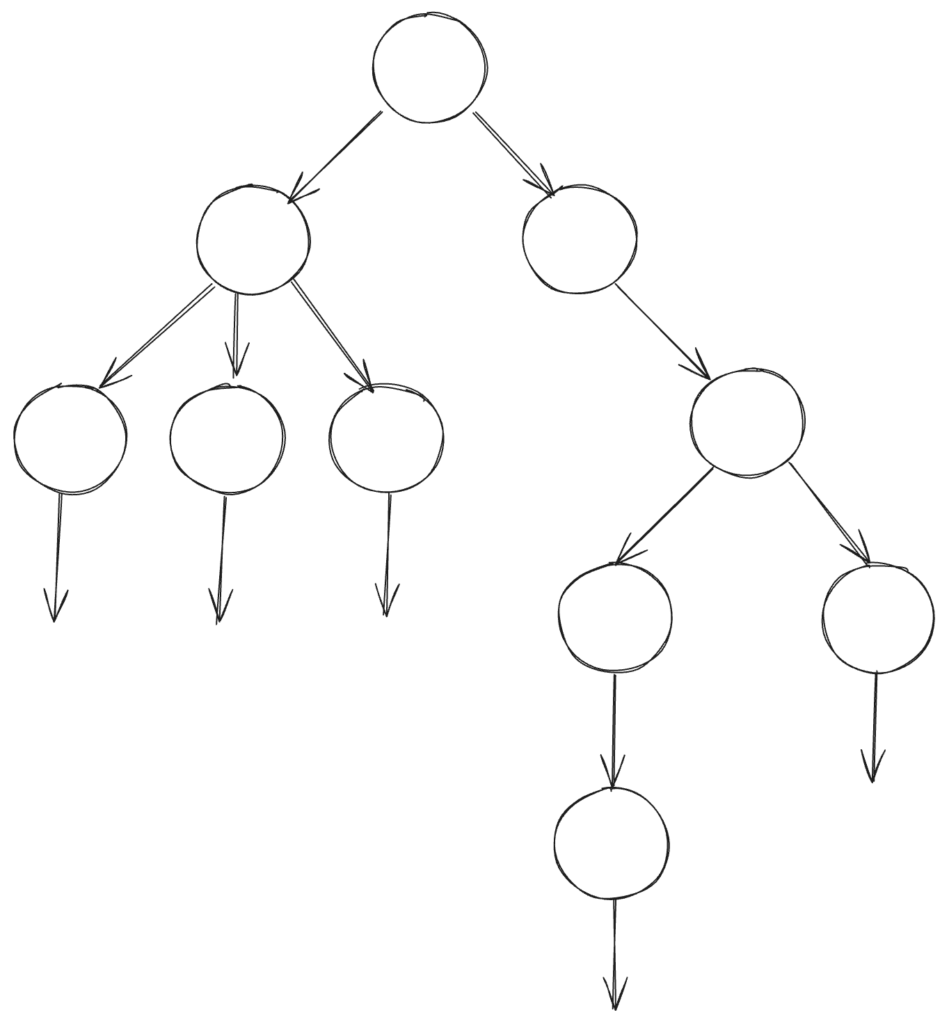
CTL では、\(X\)、\(G\)、\(F\)、\(U\) の演算子に加え、\(A\)、\(E\) の量化子を使います。
量化子とは、「すべての」や「いくつか存在する」といった概念を表現する記号です。

\(X\) は次の状態を表し、\(G\) は全ての未来の状態を表し、\(F\) はいくつかの将来の状態を表し、\(U\) は〜までということを表します。
これらの演算子は、\(A\)、\(E\) の量化子に続く形で使われます。
\(A\) は全てのパスを表し、\(E\) は少なくとも一つのパスを表します。

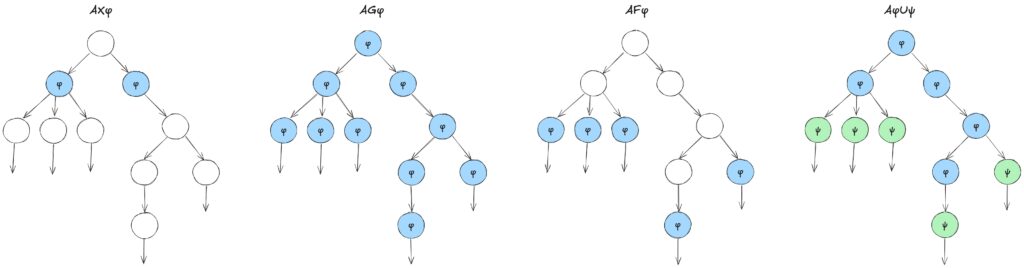
CTL では量化子を持つため、「あるパスが存在する」という性質を明示的に表現することが可能です。

2PC を用いた CTL の例

LTL で表現したような性質は、CTL では以下のように表現することができます。

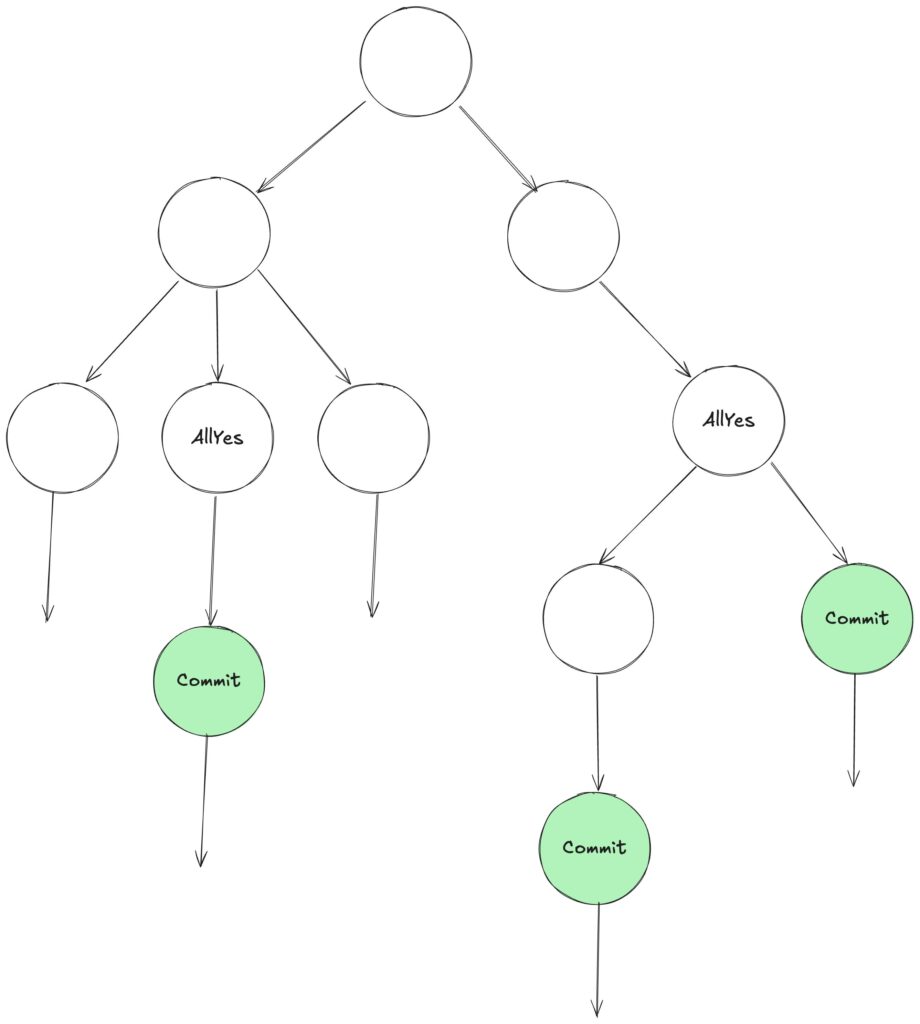
「全ての Participant が正常な応答をした場合は、最終的に Commit される。」(Liveness)

$$AG (AllYes \rightarrow AF Commit)$$

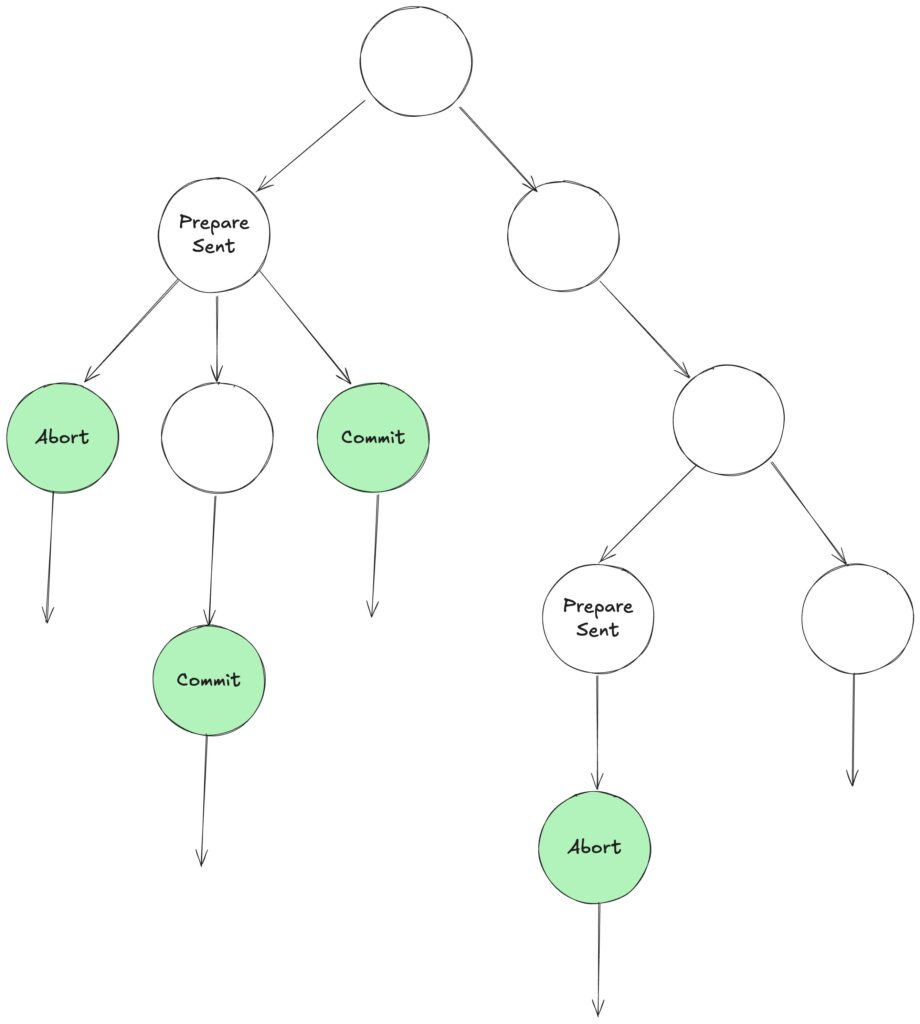
「Prepare を送信したら最終的に Commit または Abort が起きる。」(Liveness)

$$AG (PrepareSent \rightarrow AF (Commit \vee Abort))$$

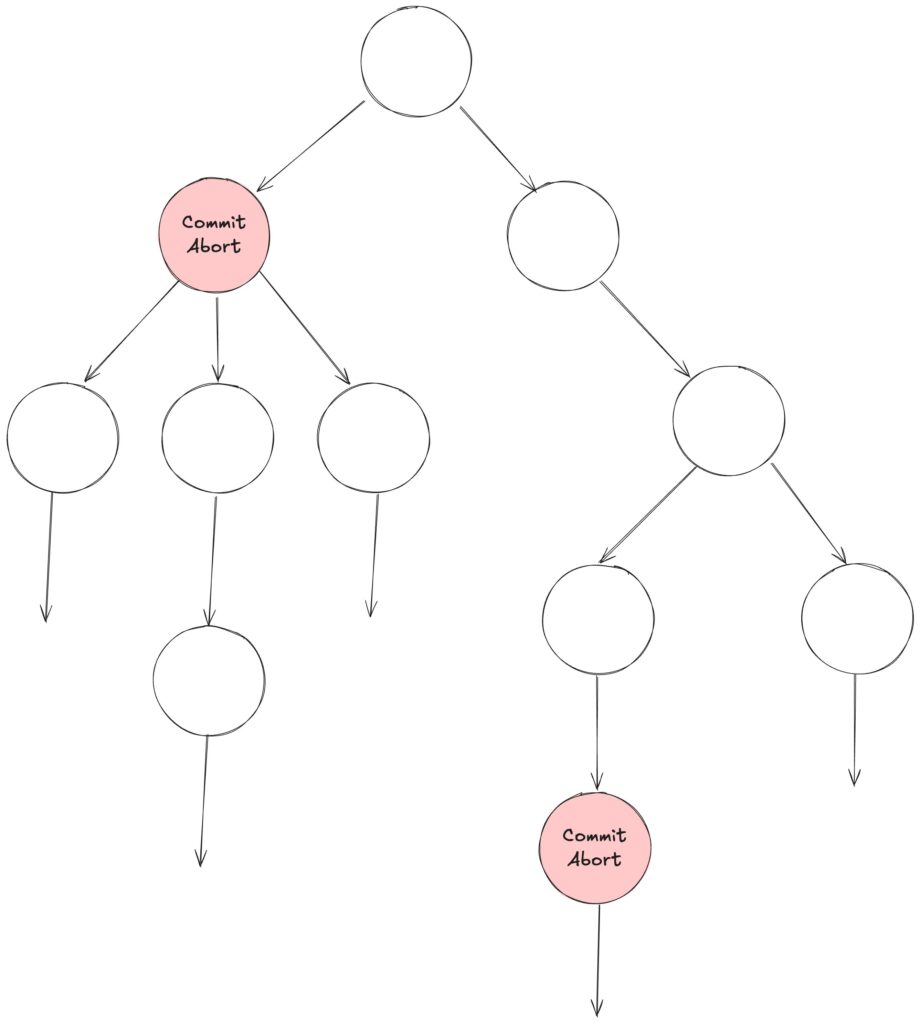
「Commit と Abort は同時に起きない。」(Safety)

$$AG \neg(Commit \wedge Abort)$$

また、CTL では以下のような、「あるパスが存在する」という性質の記述も明示的にできます。

「すべての状態から、Commit に至るパスが少なくとも 1 本存在する」

$$AG (EF Commit)$$

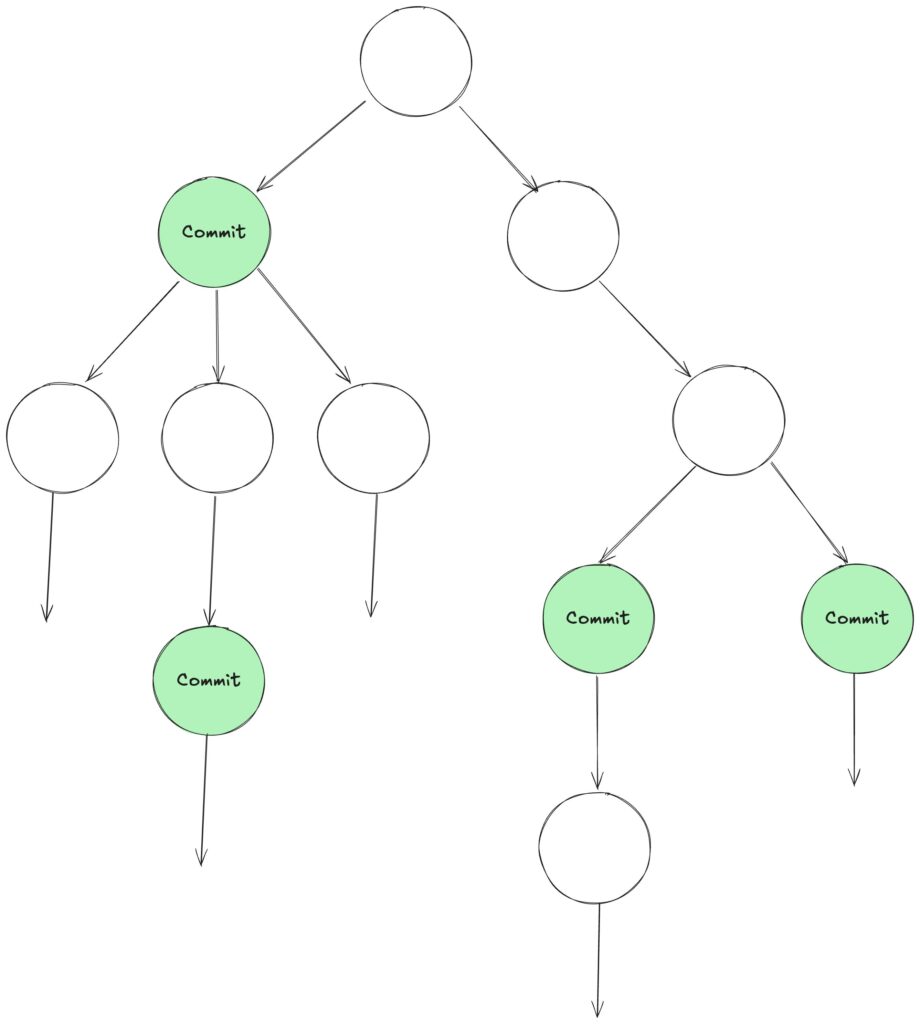
LTL と CTL はそれぞれ異なる性質記述に適しているため、目的に応じて使い分けることが求められます。

CTL を用いたモデル検査

CTL では時間を無限に続く木構造としてモデリングしますが、無限に続く木構造そのものを検査することはできません。
そのため、実際の検査の際にはこの木構造ではなく遷移システムを用いて検査を行います。
モデル検査では、遷移システム \(M\)、初期状態 \(s_0\)、時相論理式 \(\phi\) とした時 \(M,s_0 \models \phi\) が成り立つかどうかを確かめます。
これは具体的には、遷移システムの各状態に論理式を適用し遷移システムのグラフ構造を探索することで検査することが可能です。

これを解く方法として、ラベリングアルゴリズムをご紹介します。
ラベリングアルゴリズムでは以下のような手順を踏みます。

1. 最初に特定の条件を満たす状態の集合を見つけてラベル付けする
2. 状態遷移関係を使って前後の状態をたどりながらラベルを更新していく
3. ラベルの更新が収束するまで 2 を繰り返す

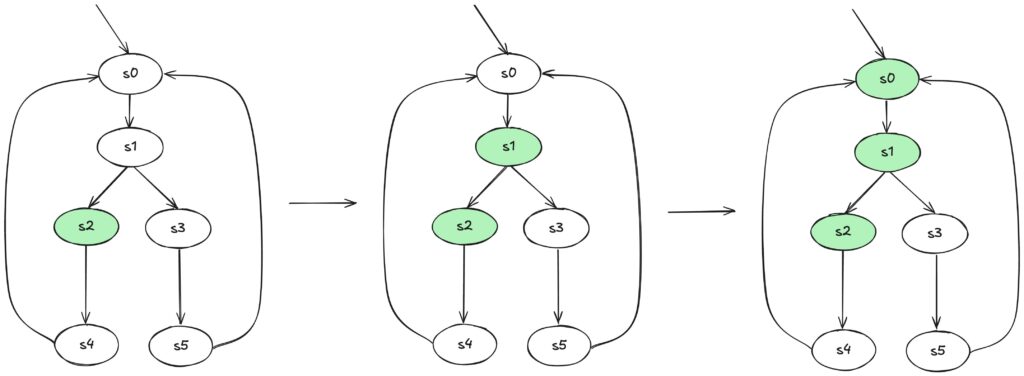
具体的にどのような条件でラベル付けしていくか、どのようにグラフを探索していくかは、各演算子によって異なるものになっています。ラベルの更新の収束後に、ラベル付けされた状態の集合について初期状態が含まれているか確認をすることで、最終的にモデルが論理式を満たしているのかどうか決定することができます。

このように、ラベリングアルゴリズムでは式の結果の真偽値を返すのではなく、「どの状態がその式を満たすか」という状態の集合を返します。これによって、複雑な論理式であってもこのアルゴリズムを使えば処理が可能です。

複雑な論理式はいくつかの部分式に分解することが可能です。例えば \(AG (EF \phi)\) は、\(EF \phi\) を評価した結果を \(\psi\) として、次に \(AG \psi\) を評価するというように分解して考えられます。
複雑な論理式によるモデル検査では、部分式の中で基本的なもの、つまりこの場合では \(\psi\)(=\(EF \phi\)) についてラベル付けを行なっていきます。
これが完了したのちに今度は、\(AG \psi\)(=\(AG (EF \phi)\)) についてラベル付けを行なっていきます。そうすると、最終的に \(AG \psi\)(=\(AG (EF \phi)\)) を満たす状態の集合を得ることができます。
このようにして複雑な論理式に対してもラベリングアルゴリズムを再帰的に適用することで、最終的な結果を得ることができます。

LTL を用いたモデル検査の方法については、本記事では扱いませんが興味がある方はぜひ調べてみてください！

未踏事業の紹介

先日、私の「ソフトウェア設計のコード化と数学的検証を実現するGoフレームワークの開発」プロジェクトが、2025年度未踏IT人材発掘・育成事業に採択されました。

「ソフトウェア設計のコード化と数学的検証を実現するGoフレームワークの開発」プロジェクトが、2025年度未踏IT人材発掘・育成事業に採択されました

このプロジェクトでは、形式手法から着想を得てgoatというソフトウェアを開発しています。

冒頭で述べたような課題に対して、設計をコードとして記述することで設計という作業そのものをより良いものにすべく取り組んでいます。

goat について

goatは、go 言語を用いて設計を記述し、その設計の正しさを検証するソフトウェアです。
goatは設計を開発サイクルの一部として統合することを目的に、以下のようなことを実現しようとしています。

• 設計をコードのように扱える体験の実現
• 設計の正しさの検証
• 設計と実装の統合

goat ではシステムをステートマシンと、キューの中を移動するイベントとしてモデリングします。

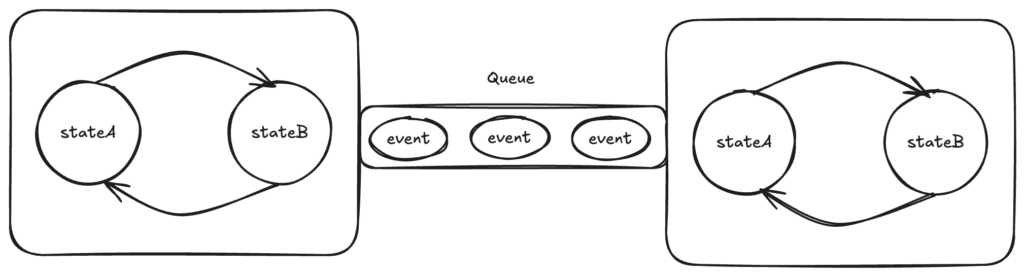
goat はユーザーの書いた設計を元に遷移システムを構築します。この遷移システムを用いて設計の正しさを検証します。
具体的にgoatでどのように設計を書くのかの記述例に関しては、こちらをご確認ください！
今はまだ時相論理には対応していませんが、今後拡張していく予定です！

goat はつい先日 v0.1.0 をリリースしました 🚀
今後も未踏のプロジェクトとして PM の皆様方や OB, OG の皆様からアドバイスをいただきながら開発していく予定です。
GitHub で Star をつけていただけると非常に励みになります！また、ぜひ皆様に使っていただいて FB をいただけると嬉しいです！

終わりに

本記事では、形式手法の入門的な内容を解説しました。
入門的な内容とはいえ数学的な概念が多く、私自身も調べながら書いていて、かなり苦戦しました。
実務で扱うにはハードルが高いとされてきた形式手法ですが、生成 AI や複雑化するシステムとの向き合い方を考える中で、いま改めて注目する意義のある技術だなと感じました。

この記事がみなさんが設計の書き方について考えるきっかけになると嬉しいです。
長文にお付き合いいただき、ありがとうございました！

参考

• Logic in Computer Science: Modelling and Reasoning About Systems,
  Michael Huth & Mark Ryan, Cambridge University Press, 2004
• ソフトウェア科学基礎 ― 最先端のソフトウェア開発に求められる数理的基礎,
  磯部 祥尚 ほか, 近代科学社, 2008