この記事は、CyberAgent Developers Advent Calendar 2025  23日目の記事です。

こんにちは、サイバーエージェントAI Lab Reinforcement Learning teamの暮石です。普段は、非定常な環境におけるバンディット問題について研究しています。

近年、ChatGPT や Gemini に代表される大規模言語モデル（LLM）は、文章生成だけでなく意思決定や推論を伴うタスクにも広く使われるようになってきました。「次に何を選ぶべきか」「どの選択が最も良さそうか」といった問いに対して、LLMがそれらしく答えてくれる場面を目にすることも多いと思います。

では、探索と活用のトレードオフを本質とする問題に対しても、LLMは本当にうまく振る舞えるのでしょうか？

本記事では、その代表例としてバンディット問題（Multi-Armed Bandit）を取り上げ、「LLMはバンディット問題を解けるか」の問いに答えることを目的として実験した結果をまとめてみたので楽しんでもらえたら幸いです。

バンディット問題とは

バンディット問題（Multi-Armed Bandit Problem, MAB）は、限られた情報のもとで逐次的に意思決定を行う問題として知られています。もう少しわかりやすくいうと「どの台が当たりやすいか分からない中で、どれを引き続けるか」を考える問題です。最初はどの台が最適かは分からないので試しながら情報を集め、その情報を使って次にどの台を選択するかを選択していく必要があります。

 

よくある問題設定は以下のようなルールの問題です。

• 複数の選択肢（腕と呼ばれる）が存在し、各腕は、未知の確率分布に従って報酬を返す
• 各ラウンドで選べる腕は1つだけ
• 選択後に、その腕の報酬だけが観測できる
• 目的は、長期的な累積報酬を最大化すること

 

バンディット問題の本質は、探索（Exploration）と活用（Exploitation）のトレードオフです。

• 活用（Exploitation）これまでの経験から「一番良さそう」な腕を選ぶこと→ 短期的な報酬は高くなりやすい
• 探索（Exploration）情報が少ない腕をあえて選び、性質を調べること→ 短期的には損をする可能性がある

活用だけを行えば、初期にたまたま当たった腕ばかり選んでしまい、より良い腕を見逃すリスクがある。一方で探索ばかり行っていても、良さそうな腕を選んでいないので累積報酬を最大化することはできません。バンディット問題では、この2つをどのようにバランスさせるかを考えます。

 

オンライン広告や推薦システムなどWebサービスの多くのアプケーションはバンディット問題として考えることができます。例えば、表示する広告クリエイティブ、表示するサムネイル、推薦するアイテムなどを腕として、クリック数や購買などを報酬として、総クリック数などを最大化させるためにどのように腕を選んでいくかを考えるかがバンディット問題に相当します。

バンディットアルゴリズムとは

バンディット問題に対するアルゴリズムは、単に「いま一番良さそうな腕を選ぶ」ためのものではありません。むしろ、どのような振る舞いを時間とともに行うべきかをあらかじめ設計したものだと考える方が分かりやすいです。

 

典型的なバンディットアルゴリズムは、次のような挙動を意図して作られています。

• 初期段階では、どの腕が良いか分からないため、広く試す（探索を多めに行う）
• 試行回数が増えるにつれて、良さそうな腕とそうでない腕が徐々に判別できるようになる
• 十分な情報が集まった後は、良いと分かった腕に選択を集中させる（活用を増やす）
• 明らかに悪い腕は、早い段階でほとんど選ばれなくなる

 

この探索と活用の切り替えがアルゴリズムの内部で

• 各腕がどれくらい良さそうかという推定値
• その推定がどれくらい不確かか（情報がどれくらい不足しているか）

を同時に管理し、「良さ」と「不確かさ」の両方を考慮して次の腕を選ぶように設計されています。こうした考え方を、非常にシンプルな仕組みで実装した代表的なアルゴリズムとしてThompson Sampling（TS）などが挙げられます。

 

ここから本題です。

LLMは、最初はどの台が最適かは分からない状態で試しながら情報を集めていき、累積報酬を最大化できることができるのでしょうか？

本記事では、この問いに答えるために実験していきたいと思います。

実験設定

本章では、前章で述べた問い「LLMはバンディット問題を解けるのか」に答えるために行った実験の設定を説明します。

問題設定

扱う問題は、2腕ベルヌーイのバンディット問題です。

• 腕は 2 つ（0 と 1）
• 各腕は、それぞれ固定された確率（アーム0：0.3、アーム1：0.25）で報酬 1 を返す（報酬は 0 or 1 のみ）
• 各ラウンドで選べる腕は 1 つ
• 目的は、累積報酬を最大化すること
• 各実験は500 iteration実行し、seed値を変更して20回実験を行った
• 評価は累積後悔（「最初から最適な腕を選び続けていた場合」と比べて、どれだけ損をしたかを表す指標）で行う

比較対象

実験では、以下の手法を比較します。

• Thompson Sampling（TS）: 探索と活用が理論的にうまく設計されたバンディットアルゴリズム
• LLM による腕選択 : 履歴をテキストとして与え、次に選ぶ腕を LLM に決定させる方法

Thompson Sampling は、探索と活用を適切に行えるベースラインとして用います。
LLMには、Geminiの gemini-2.5-flash-liteを用いています。

LLMによる腕選択の方法

LLM には、これまでの履歴を テキスト形式で与えます。

履歴は次のような形式です。

t,arm,reward
0,1,0
1,0,1
2,0,1

各行は、

• t : ラウンド番号
• arm : 選択した腕
• reward : 観測された報酬（0 または 1）

を表しています。

 

LLM には、この履歴のみを渡し、

次に選ぶべき腕（0 または 1）を 1 文字で返す

ように指示します。

実験結果

本章では、前章の設定のもとで得られた実験結果を示し、LLM と Thompson Sampling（TS）の挙動の違いを、主に累積後悔（Cumulative Regret）の観点から比較したいと思います。

累積後悔による比較

まず、各手法について累積後悔を計算し、iteration に対する推移を比較しました。

以下の図が各手法の累積後悔をまとめた結果です。

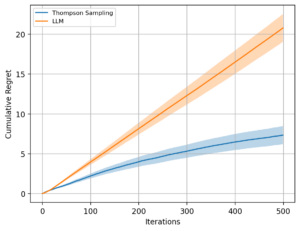
500iterationという少ない期間ではありますが結果として、次のような傾向が確認できます。

• Thompson Sampling（TS）
  • 累積後悔は iteration の増加に対して 緩やかに増加
  • 全体として 対数オーダー（log T）に近い挙動
• LLM による腕選択
  • 累積後悔は iteration に比例して ほぼ線形に増加
  • iteration が進んでも後悔の増加が止まらない

この結果をまとめると、LLMでは報酬が高い腕に収束していくような挙動はしていないということになります。

各アルゴリズムの挙動の比較

次に、各手法について時間が進むにつれてどのアームを選択するようになっていくかを比較しました。理想的には、良いアームに時間が進むにつれて収束していくのが望ましい挙動であり、理想と比べてどうかを確認します。

具体的には、iterationごとにウィンドウ幅100size分の結果を平均したものを可視化しました。

以下の図が各手法のiterationごとのアームの選択確率の推移です。

Thompson Samplingのiterationごとのアームの選択確率の推移

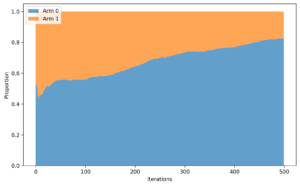
LLMのiterationごとのアームの選択確率の推移

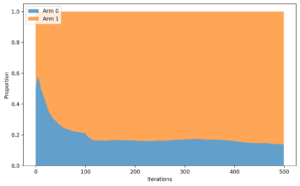
500iterationという少ない期間ではありますが結果として、次のような傾向が確認できます。

• Thompson Sampling（TS）
  • アームの選択確率は緩やかにアーム１に収束していく
  • 最初はランダムに近いが、少しずつアーム１を選択するようになっていく
• LLM による腕選択
  • 初期段階で一方の腕を高く評価すると、その腕に選択が偏りやすい
  • 探索が十分に行われないまま、早期に一方の腕へ張り付く挙動が見られる
  • アームの選択はシードによって、固定されている事象が見受けられる
  • 今回の結果では、たまたま悪いアームの方を選ぶシードが多い

この結果をまとめると、LLMではランダム性を「ノイズ」ではなく「戦略」として扱うこと自体が難しいことがわかります。

 

まとめ

本記事では、「LLMはバンディット問題を解けるのか」という問いに対して、2腕ベルヌーイバンディットを用いた実験を通じて検証を行いました。累積後悔を指標として Thompson Sampling（TS）と比較した結果、TS は理論通り累積後悔が log T オーダーに抑えられる一方で、LLM による腕選択では累積後悔がほぼ線形に増加することが確認できました。

 

この差は、探索の扱い方の違いに起因していると考えられます。

• TS では不確実性が確率分布として明示的に管理され、その分布からのサンプリングによって探索と活用が同時に実現されている。
• LLM では、履歴をテキストとして解釈することはできても、不確実性やランダム性を戦略的に扱う仕組みを内在的には持っていない。その結果、探索は偶発的になりやすく、長期的には後悔が蓄積し続ける挙動になってしまう。

また、実験を通して、LLM にとってランダム性を「ノイズ」ではなく「戦略」として扱うこと自体が難しいことも確認できました。

 

本記事では扱いませんでしたが、実際の応用を考えると、推論速度や API 呼び出しコスト、コンテキスト長の制限といった実務的な問題も無視できません。バンディット問題のように毎ラウンド意思決定が必要な設定では、これらの制約はアルゴリズム選択に大きく影響します。

以上を踏まえると、LLM をバンディット問題の意思決定器として直接用いるのは、現時点では安定性・理論的性質の両面で課題が多いと言えそうです。本記事をきっかけにバンディット問題により興味を持つ人が増えましたら幸いです。