AI 事業本部 Dynalyst の ML エンジニアの川瀬です。
普段は Dynalyst で広告配信アルゴリズムの開発を行っているのですが、今回は弊社のゼミ制度の下で活動している量子コンピュータゼミの紹介をしようと思います。
量子コンピュータゼミ
CyberAgent にはゼミ制度というものがあり、今後の事業成果につながる可能性のある領域における研究活動が支援されています。現在、社内ではさまざまなゼミが開かれており、量子コンピュータゼミでは量子コンピュータの将来的な応用に向けたリサーチを行っています。
この数年で量子コンピュータへの注目度は飛躍的に高まっていますが、実社会への応用という面では解決すべき課題が残っていることも事実です。量子コンピュータゼミでは、これからの技術的進歩を見据えて、現時点で貢献できることを見つけようというスタンスで活動しています。
量子ゲーム
量子コンピュータゼミでは、その活動のひとつとして量子コンピュータを利用したゲームの開発を行っています。以下では、ゼミ活動の中で考案した量子ポーカーというゲームの紹介をします。
目的
まず、なぜ量子コンピュータを利用したゲームを考案しようと思ったのか、その目的を説明します。
最近は量子コンピュータのニュースを目にする機会が多くなってきましたが、具体的に量子コンピュータがどのようなものか知っている方はそれほど多くないのではないでしょうか。その理由としては、量子コンピュータについて理解するためには量子力学の知識が必要となるため、物理学に詳しくない方にはハードルが高いことが挙げられます。
しかし、量子コンピュータのように本質的に新しい技術には、難しそうだという理由で敬遠するにはもったいない魅力があります。そこで、物理学の知識のない人が心理的な抵抗を持たずに量子コンピュータに触れることができる機会を提供するために、ゲームという手段を考えてみることにしました。ゲームを遊ぶことで、科学に楽しみを見いだすきっかけが得られるようなものが作れるといいなと思っています。
アイディア
次に、今回考案した量子ポーカーがどのようなアイディアに基づくものか、概要を簡単に説明します。
量子ポーカーは、一人用のビデオポーカー(ドローポーカー)の量子コンピュータ版といえるものになっています。ビデオポーカーは、配られた 5 枚のカードのうち、交換するカードを好きなように選んでポーカーの役を作ることを目指す単純なゲームです。
ビデオポーカーでは、交換するカードの選択肢を古典的な論理回路で表現することができます。つまり、5 枚のカードそれぞれに対応する 5 つの論理ビットを用意して、カードを残す場合は 0、交換する場合は 1 となるように値を設定することで、プレイヤーの選択肢を表すことが可能です。5 つの論理ビットの初期値が 0 に設定されているとすると、NOT ゲートによって論理ビットを適当に反転する回路を作ることがプレイヤーの戦略となります。
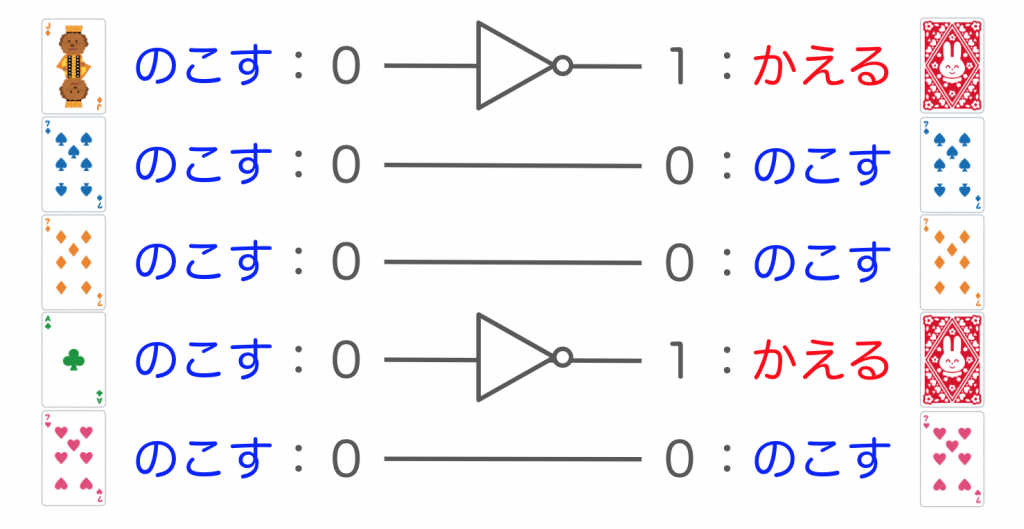
この論理回路を量子回路に置き換えることで、量子コンピュータ版のビデオポーカーを実現できるというのが、量子ポーカーのアイディアとなっています。
量子回路
唐突に量子回路という単語を出しましたが、いわゆるゲート式量子コンピュータでは、量子回路を用いて計算が行われます。量子回路では、古典的な回路の論理ビットと論理ゲートの代わりに、量子ビットと量子ゲートが使われる点が特徴です。
量子ポーカーの話題の前に、量子ビットと量子ゲートについてざっくりと説明してみようと思います。ここではあまり込み入った解説はできないので、詳細が気になる方は教科書や他のサイトの記事などを参照いただくことをおすすめします。
量子ビット
まず、量子回路の入出力の状態を表す基本的な単位である量子ビットを紹介します。
古典的な論理ビットの場合、それらが 0 か 1 のどちらか一方の値を常に保持していることは明らかです。一方、量子ビットの場合、値の観測結果が 0 となる状態と 1 となる状態の重ね合わせ状態の存在が許されています。したがって、量子ビットの値は観測を行う前には特定することができず、観測を行った際にそれぞれの値が得られる確率のみを知ることができます。
量子ゲート
量子ビットに対する操作には、量子ゲートが用いられます。ここでは代表的な 3 つの量子ゲートを紹介します。
X ゲート
1 つの量子ビットに対して操作を行う量子ゲートとして、直観的に一番わかりやすいのが X ゲートです。
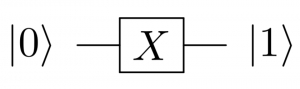
X ゲートは、観測結果が 0 となる状態(状態 0)を観測結果が 1 となる状態(状態 1)に移すように働く量子ゲートとなっています。これは古典的な NOT ゲートに対応するような挙動をする量子ゲートであると考えられます。
H ゲート
1 量子ビットに対して操作を行う量子ゲートには、アダマールゲート(H ゲート)と呼ばれるものもあります。
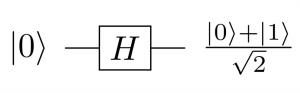
状態 0 に H ゲートを適用した状態は、状態 0 と状態 1 の重ね合わせ状態です。すなわち、この状態を観測すると、観測結果は次のようになります。
- 50% の確率で観測結果は 0 となる。
- 50% の確率で観測結果は 1 となる。
H ゲートを導入することで、量子コンピュータに特有の重ね合わせ状態を作り出すことができます。
CNOT ゲート
論理回路の場合、AND ゲートや OR ゲートのように複数ビットを入力とする論理ゲートが存在しますが、量子回路の場合にも複数量子ビットに対して操作を行う量子ゲートがあります。
CNOT ゲートは、制御(Control)量子ビットと標的(Target)量子ビットと呼ばれる 2 つの量子ビットに対して操作を行う量子ゲートです。このゲートには、制御量子ビットが状態 1 の場合のみ標的量子ビットを反転するという性質があります。
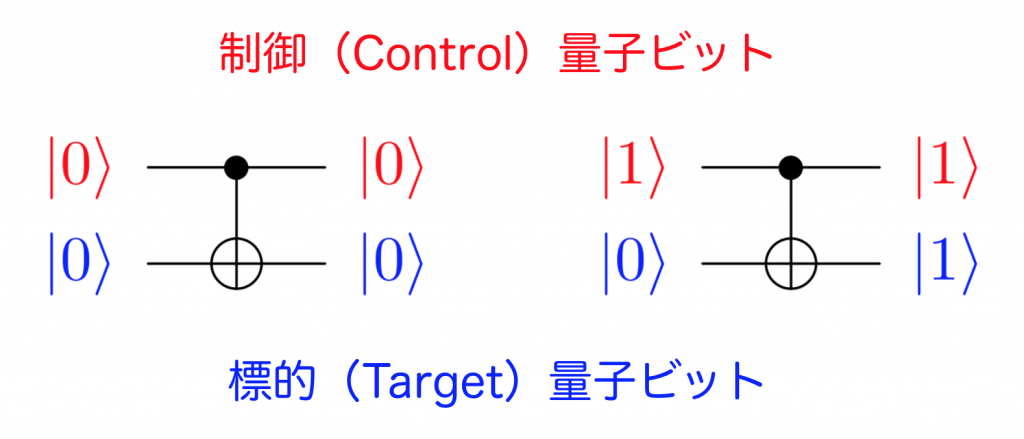
1 量子ビットを操作する量子ゲートと CNOT ゲートを組み合わせることで、さまざまな量子回路を自由に作ることができます。
量子ポーカー
一応これで準備ができたので、量子ポーカーの話題に戻りましょう。
量子ポーカーでは、ビデオポーカーのカード交換を量子ゲートを使って記述します。ビデオポーカーが NOT ゲートを用いた論理回路で記述できたことを思い出すと、X ゲートのみを用いた量子回路によって古典的なビデオポーカーを再現できることがわかります。さらに、X ゲート以外の量子ゲートも利用することで、カード交換のルールが拡張された量子ポーカーとなります。
量子ポーカーと普通のビデオポーカーは何が違うのか、具体例で見てみましょう。
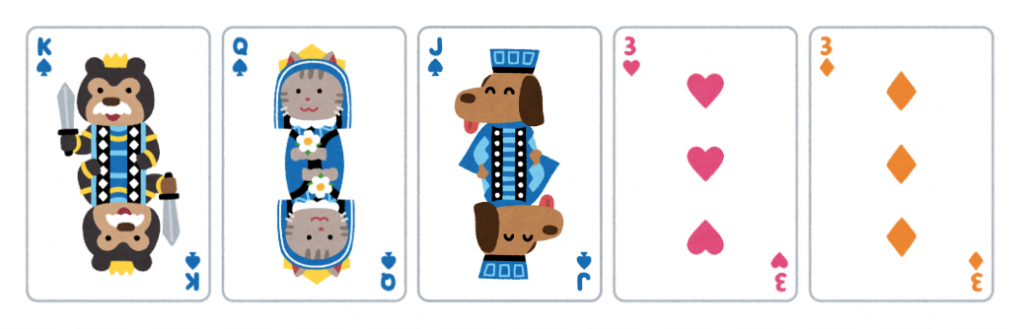
最初にこれらのカードが配られた場合、カード交換でポーカーの役を成立させるためにはどのような選択肢があるでしょうか。
- スペードのロイヤルストレートフラッシュを狙う?
- 3 のワンペアを確保する?
普通のビデオポーカーの場合、どちらか一方の狙いを選択して、もう一方は諦めるしかありません。つまり、3 のペアを交換するか交換しないか、どちらかを選択する必要があります。
一方、量子ポーカーでは、3 のペアを交換する場合と交換しない場合の重ね合わせ状態を構成することで、両方の狙いを同時に生かしておくことができます。
では、具体的にどのような重ね合わせ状態を作ればいいのでしょうか。今回のケースを見ると、交換すべきカードには以下のような制約があることに気が付きます。
- ハートの 3 を残すならば、ダイヤの 3 も残したい。
- ハートの 3 を交換するならば、ダイヤの 3 も交換したい。
実は、H ゲートと CNOT ゲートを組み合わせることで、このような制約を満たす重ね合わせ状態を作ることができます。
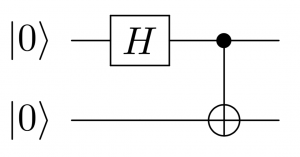
この量子回路で作られる状態はベル状態と呼ばれるもので、次のような性質を持ちます。
- 一方の量子ビットの観測結果が 0 のとき、もう一方の量子ビットの観測結果も 0 である。
- 一方の量子ビットの観測結果が 1 のとき、もう一方の量子ビットの観測結果も 1 である。
この性質は量子もつれ(エンタングルメント)と呼ばれ、量子コンピュータにおける最も重要な性質のひとつとなっています。
このように、量子コンピュータの性質を利用することで、ゲームの戦略に幅を持たせることができます。
実装
今回の記事で解説した量子ポーカーですが、ゼミのメンバーが実装した試作品があるので紹介します。ゲーム性を増やすためのルールに改善の余地はあるのですが、とりあえずコンセプトを表現したものとなっています。
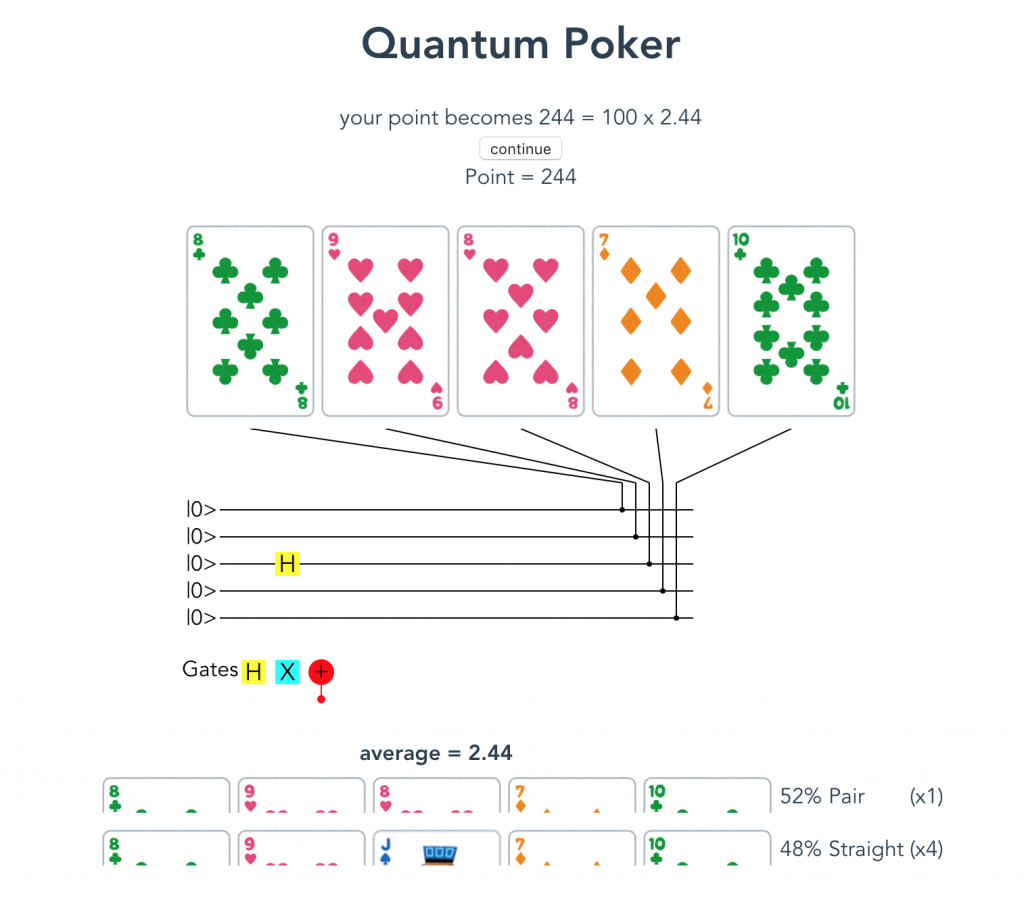
このゲームでは、最初に配られたカードに対して量子回路を作成します。作成した量子回路に対して量子ビットの観測を繰り返し、完成した役に応じて得られる得点の平均値が配当となります。
今回の実装では、量子コンピュータの挙動をシミュレーションする TypeScript のライブラリとして qramana が利用されています。このライブラリは、ゼミメンバーの一人が加わっている未踏ターゲット事業にて開発されたものです。
まとめ
量子コンピュータゼミでは、量子コンピュータについて知るきっかけとなるゲームを作ろうという目標で量子ポーカーを考案しました。予備知識のない方への導入とするにはまだ改善が必要なのですが、ゲームを入り口とするという方向性は間違っていないと思っています。
これからも、科学の面白さを人々に広めることができるような活動をゼミでやっていきたいと考えていますので、また何か紹介できる機会があればよろしくお願いします。
