こんにちは、AI事業本部 Dynalyst所属のデータサイエンティストをしている藤田です。今回は内定者バイトとしてDynalystにて働いて頂いた黒岩さんからの寄稿記事です。
以下本文です。
AI事業本部のDynalystで、機械学習エンジニアとして一ヶ月間内定者バイトをしていた黒岩です。広告配信の最適化手法と内定者バイトで取り組んだ課題について紹介します。
広告配信の最適化
広告配信では、複数の候補の中から一つの広告を選んで広告枠に表示します。この時、ユーザのクリック数の合計を最大化するように広告を選びたい、というのが今回の問題設定です。
単純に考えれば、これまでのデータから計算されるクリック率(CTR)が最も高い広告を選べば良さそうなものです。しかし、CTRを計測するためには全ての広告をある程度の回数表示してデータを集める必要があるので、この過程でCTRの低い広告も表示することになります。したがって、CTRの高い広告ばかりを表示したいが、CTRの高い広告を知るためには他の広告も表示しなければならない、というトレードオフがあります。このバランスをうまくとって、クリック数を最大化したいです。
多腕バンディット問題
前述の広告配信の最適化は、強化学習の問題設定の一つである、多腕バンディット問題としてモデル化することができます。
多腕バンディット問題(multi-armed bandit)では、N個のスロットマシンがあり、スロットマシンの腕を引くと一定の確率で当たって報酬を得ることができます。この腕を引く行動をここでは「試行」と呼びます。T回の試行回数の中で、得られる報酬の和を最大にしたい、というのが多腕バンディット問題の設定になります。
スロットマシンが広告の候補、当たる確率がクリックされる確率、クリックされれば報酬1でされなければ報酬0がもらえる、とすれば広告配信の最適化を多腕バンディット問題でモデル化することができます。また、前述の広告配信におけるトレードオフは、強化学習では「探索と活用のトレードオフ」(exploration-exploitation trade-off)として広く知られています。
Thompson Sampling
多腕バンディット問題に対する手法の一つにThompson Sampling(TS) (Thompson, 1933))があります。TSは単純な手法ながら、実験的には高いパフォーマンスを誇ることが示されています(Li and Chapelle, 2011)。以下にTSの手順を説明します。
- 各スロットマシンが当たる確率を確率分布で推定する
- 各試行では、スロットマシン毎に確率分布から値をサンプルし、その値が最大となるスロットマシンの腕を引く
- 腕を引いた結果を使ってそのスロットマシンが当たる確率の確率分布を更新する
Li and Chapelle(2011)で紹介されている手法では、確率分布としてベータ分布を用います。ベータ分布はaとbの二つのパラメータを持ち、期待値がa/(a+b)、分散がab/(a+b)2(a+b+1)になる確率分布です。ベータ分布の例を画像に示しました。左側がa=b=5、右側がa=b=100です。両方とも期待値は1/2と同じ値ですが、右側の方が山が中心に集中していることがわかります。これは、aとbが大きくなるほど分散が小さくなるからです。
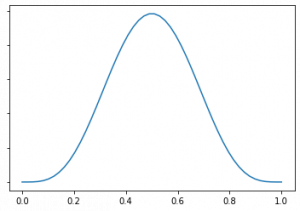
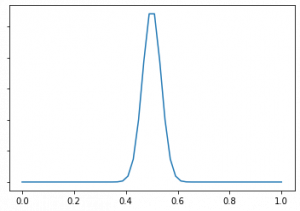
ベータ分布をスロットマシンが当たる確率の推定に使います。当たった回数をaとし当たらなかった回数をbとすれば、確率分布の期待値はこれまでのデータでの当たった確率a/(a+b)に一致します。そして、試行回数が増えるほど分散が小さくなって、推定の確からしさが増していきます。
TSにおいて、試行回数が少ないうちはどのスロットマシンのベータ分布も分散が大きいので、サンプルされる値も期待値からばらついて、比較的ランダムにスロットマシンの選択が行われます。一方で、試行回数が増えると分散が小さくなるので、期待値の大きいスロットマシンが選ばれやすくなります。TSはこのようにして探索と活用のトレードオフのバランスをとります。
多腕バンディット問題によるモデル化の問題点
多腕バンディット問題によるモデル化は、実際の広告配信にある性質を少なくとも2つ無視しています。
- 広告がクリックされる確率はユーザの属性によって異なる
- 広告がクリックされる確率は時間によって変化する
1については文脈付き多腕バンディット問題(contextual multi-armed bandit)というモデルが、2については非定常な多腕バンディット問題(non-stationary multi-armed bandit)(Gur et al., 2014)というモデルが存在します。
ユーザの属性を用いたThompson Samplingの改善
Dynalystでは広告配信の一部でTSを使っていました。しかし、前述のように多腕バンディット問題によるモデル化は広告配信のいくつかの性質を無視しています。そこで内定者バイトでは1の性質に着目し、ユーザの属性に応じた広告配信の最適化に取り組みました。
Li and Chapelle(2011)では、文脈付きバンディット問題にTSを拡張した手法が紹介されていますが、今回はより単純な手法を試すことになりました。具体的には、クリックしやすい広告が異なる傾向を持つようにユーザをクラスタリングし、クラスタ毎にTSを行うというものです。この手法をClustered Thompson Sampling(CTS) と呼ぶことにします。
CTSの有効性を確認するために、ユーザの属性によってクリックされやすい広告の傾向が変わるのかを調べました。各ユーザは多次元のベクトルで表され、各次元が何らかの特徴量に対応します。ここから一つ特徴量を選び、値の範囲に応じてユーザを数個のクラスタに分類し、クラスタ毎にクリックされやすい広告を調べました。ここでは有意水準5%のカイ二乗検定と残差分析を用いて、クラスタ内で有意にクリックの頻度が高い広告を特定しました。このクリックの頻度が高い広告がクラスタ間で異なる場合は、CTSによるクリック数の増加を期待できます。
本番環境のログを分析した結果として、ある特徴量に基づいてユーザを3つのクラスタに分けるのが有効ではないか、ということがわかりました。
本番環境でのA/Bテスト
Dynalystには既にTSが一部の広告配信で運用されていたため、そのコードを利用しながら、前述の分析に基づいたCTSを実装しました。
Dynalystでは、日々本番環境でのA/Bテストによって様々なものの評価と改善を行っています。今回も、広告配信の一部を使ってCTSとTSとのA/Bテストを行いました。時間の都合上、A/Bテストの期間は4日程度となりました。
A/Bテストの結果、全体ではCTRは減少してしまいました。実際には、表示できる広告の候補は広告主と広告枠のサイズ(これを合わせて設定と呼びます)毎に決まっています。そこで、より詳細に比較を行うため、設定毎にCTRを比較し、有意水準5%のカイ二乗検定を行いました。結果として、CTSがTSより有意に良かった設定はなかった一方で、TSがCTSより有意に良かった設定がいくつか存在しました。
したがって、少なくとも現状の結果ではCTSがTSに劣っているということが言えます。
この原因を考えるために、CTSがTSに有意差をつけられてしまった二つの設定で、TSとCTSの挙動を可視化してみました。
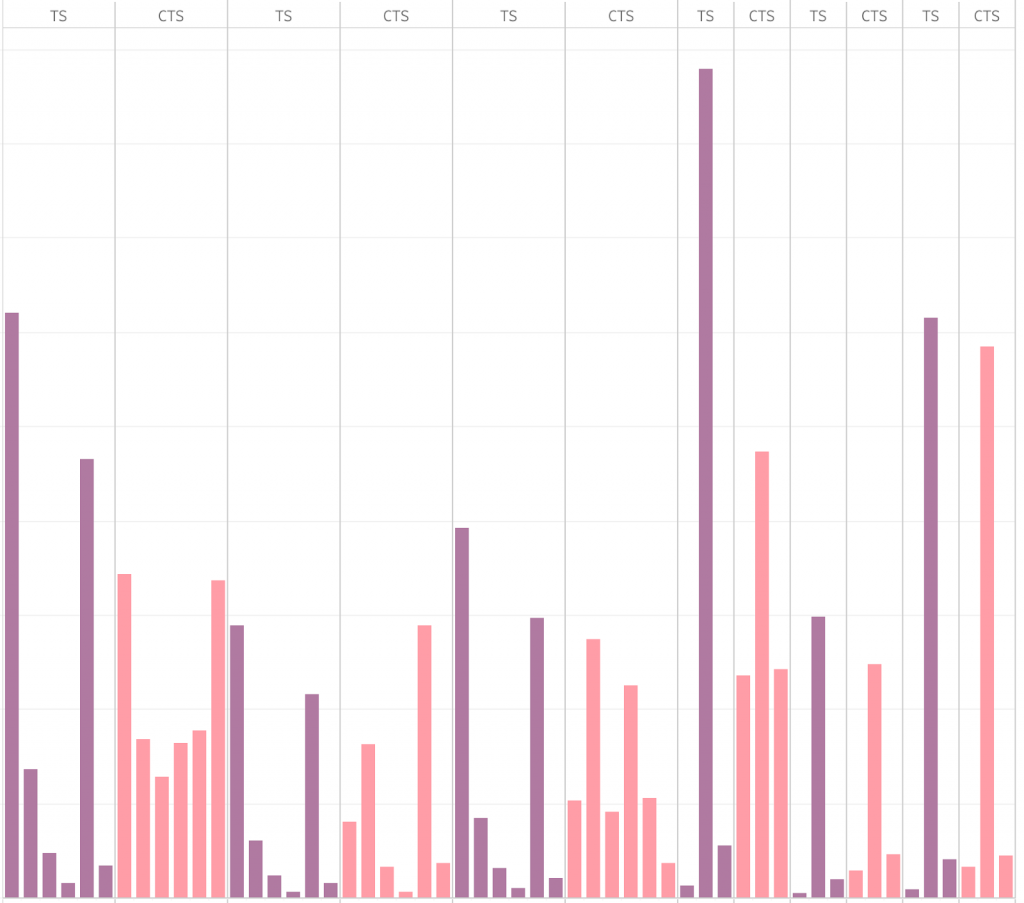
上のグラフは、二つの設定について、ユーザクラスタごとにどの広告を表示したかの回数を可視化したものです。TSの結果が濃い紫色でCTSの結果がピンク色で表示されています。左から六番目までの棒グラフが一つの設定で、それより右は別の設定です。例えば一番左の二つの棒グラフは、ある設定のあるユーザクラスタでTSとCTSが表示した広告の分布を表しています。
全体的に、TSの方が表示する広告の偏りが大きく、一つの広告ばかり出す傾向にあります。これはTSが探索した結果から活用を行っていることを示しています。一方でCTSはTSより表示する広告のばらつきが大きく、一つの広告に絞り切れていない傾向が伺えます。
CTSではクラスタ毎にデータが分割されるため、TSと比べると利用できるデータの量が少ないです。そのために探索が十分に行えず、有効なテンプレートを絞り込んで活用することができていないのではないかと考えられます。
現状では、TSとCTSがともに現在時刻から過去三日分のデータを利用するようにしています。CTSに探索を十分に行わせるためには、この集計期間を延長した方が良いかもしれません。ただし集計期間を延長した場合、直近の傾向を反映できない可能性があります。適切な集計期間を見つけることは今後の課題です。
あるいは、別の特徴量に注目したより良いクラスタリング方法があるかもしれません。
また、Chapelle and Li(2011)で提案されているような、文脈付きバンディット問題に対する手法では、ユーザをクラスタに分割せずに全てのデータを学習に使うことができます。こういった手法を実装しA/Bテストを行うことも今後の課題です。
まとめ
今回の取り組みでは、残念ながら広告配信の最適化手法を改善するには至りませんでしたが、今回のA/Bテストの結果がより良い手法の選定や開発につながればと思います。
手法の改善という部分では結果を出せませんでしたが、A/Bテストを行っていく中で、既存のThompson Samplingの実装のバグを見つけて修正し、挙動を改善させることができました。この点では自分なりにDynalystに貢献することができたのではないかと思います。
内定者バイトの感想として、一ヶ月という短い期間ながら手法の実装とA/Bテストを経験できたことは、非常に面白い経験でした。Dynalystの皆さんは、適切にタスクを切り出して、データ分析や実装など様々な面でサポートしてくださいました。メンターの藤田さんをはじめ、Dynalystの皆さん、本当にありがとうございました。サイバーエージェントで働いた期間はとても楽しく、たくさんの学びを得ました。
最後に、サイバーエージェントの内定者である私ですが、海外の大学院の博士課程への進学を目指して出願していました。会社の方のご厚意で、その合格発表を待ってから進学か就職かの進路を決めてよいという話になっていました。内定者バイト期間の最終日にある大学から合格通知をもらったため、就職ではなく進学の道を選ぶこととしました。そのため、この記事は実は内定者ではなく元内定者の記事ということになります。一内定者の事情に寛大に合わせてくださったことに本当に感謝しています。
参考文献
Chapelle and L. Li. An Empirical Evaluation of Thompson Sampling. In Advances in Neural Information Processing Systems 24, pages 2249–2257, 2011.
R. Thompson. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3–4), pages 285–294, 1933.
Gur, A. J. Zeevi, O. Besbes. Stochastic Multi-Armed-Bandit Problem with Non-stationary Rewards. In Advances in Neural Information Processing System 27, pages 199-207, 2014.

