概要

同じ介入を比較するA/Aテストで統計的に有意な差が出てしまうケースがある
その原因は、A/Bテストの指標の設計に失敗していることかもしれない
この問題の対処法としてユーザベースCTR、デルタメソッド、クラスターロバスト標準誤差を紹介する
これらの手法は実務で運用する上では一長一短

はじめに

AI事業本部Dynalystの伊藤、小売セクターの藤田(@6km6km)です。 DynalystはReal Time Biddingと呼ばれる広告オークションにおいて広告枠の買付を行うプラットフォーム（DSP: Demand Side Platform）です。DSPでは、ユーザに広告を表示する際に複数あるクリエイティブの候補からひとつクリエイティブを選ぶ必要があり、その選択ロジックにバンディットアルゴリズムを用いています。（参考リンク1, 2）

以下では、バンディットアルゴリズムのA/Bテストをする際に生じた問題について紹介します。本記事の一部はDynalystの業務にインターンとして関わっていただいた慶應義塾大学の筧悠夫さん、トロント大学の黒岩稜さんの貢献によるものです。

余談

@po3rinさんが書かれたエムスリーアドベントカレンダーとまさかのネタ被りをしてしまいました…。マニアックなネタだと思っていたので驚きましたが、みんな似たようなことで悩んでるんだなと勝手に一体感を感じました（聖書Trustworthy本[1] 万歳！）。幸い、@po3rinさんと本記事で焦点を当てているポイントが違っていたので、そのままのネタで公開させていただきます。

検索エンジンのABテストで発生するユーザー内相関を突破する – エムスリーテックブログ

設定

背景

既存のバンディットアルゴリズムを改良した手法の導入を検討している
オフライン評価（参考リンク3）において精度の向上が確認できたので、A/Bテストでオンラインでの性能を評価したい

分析内容

ユーザをランダムに2群に分割し[2]、A/Bテストを実施する
KPIはクリック率(CTR: Click Through Rate) = 総クリック数 / 総インプレッション数 [3]
A/Aテストによって、A/Bテストが正しく動作していることを保証する

A/Aテストが失敗する？

Webサービス上でA/Bテストを実施するにあたって、まずテストの結果が信頼できることを確認する必要があります。例えば、ユーザをAとBに割り当てるロジックに偏りがある、ロギングが正しくされていない、AとBでリダイレクト速度が異なるなど、システムのバグが発生するかもしれません。その結果、本来は差がない結果を差がある（もしくはその逆）と結論づけてしまう恐れがあります。

これを回避するために、A/Aテストが用いられます。A/Aテストでは、通常のA/Bテストのようにユーザをランダムに2群に分割しますが、各群に同じ介入(AとA)を割り当てます。再掲ですが@po3rinさんの「AAテストのアーキテクチャ」の図がわかりやすいので参考にしてください。

検索エンジンのABテストで発生するユーザー内相関を突破する – エムスリーテックブログ

A/Aテストにおいては同じ介入を割り当てているわけですから、その2群間でのユーザ行動が等しいことはほとんど自明です。そのため、テストが正しく設計されていれば、両者の結果に差がないことが期待されます。逆に差があるケースでは、システム上のバグや集計ミス、評価指標の計算方法が不適切であることを疑います。

Dynalystのクリエイティブ選択ロジックにおいても、既存バンディットアルゴリズム(A)と全く同じもの(A’)に50%:50%でユーザを割り当てるA/Aテストを実施しました。本番環境で一定期間配信した結果を分析すると、AとA’のクリック率に統計的に有意な差があり[4]、A/Aテストが失敗しました。異なる期間で配信したり、ユーザの割当に用いるハッシュ関数を変えるなどしてもA/Aテストが失敗したため、詳しく調べることにしました。まず、システムのバグを疑いましたが、怪しい箇所は見当たらなかったので配信ログを深掘りしたところ、時系列でクリック率をプロットすると明らかに突出した点が存在することが判明しました。

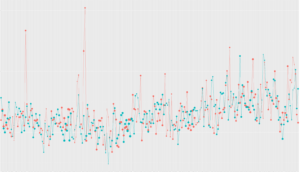
ロジックA（赤）とA'(青)のクリック率の時系列推移（縦軸: クリック率、横軸: 時間）。ロジックAで明らかに突出した点が存在することが確認できる

突出点をユーザ単位で集計してみると、一部のヘビーユーザ[5]がたくさんインプレッションしたりクリックしていることがわかりました。そこで、ヘビーユーザを適当な条件で除外して再集計すると突出点がなくなりました。検定においても統計的な有意差がなくなったことを確認しています。

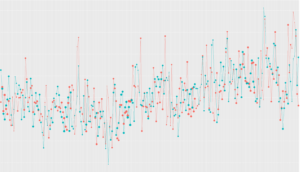
それでは、ヘビーユーザを除外して分析を行えばよいのでしょうか？必ずしもそうはなりませんでした。ヘビーユーザを除外するためには何かしらの除外ルールを設ける必要がありますが、そのルールを色々試行錯誤していると、その度にp値が小さくなったり大きくなったりしてしまいました。そうなると除外によってA/Aテストが成功したとしても、設けた除外ルールによってp-hackingを行っているだけであるという謗りから免れません。また、そもそもヘビーユーザの影響を除外したものがビジネス的に評価したいKPIなのか？という疑問もあります。

このように（成功することが自明な）A/Aテストであっても実務においては案外失敗してしまうのです。DynalystでのA/Aテストの失敗はしばしば発生し、その原因も多岐にわたります。

そのような状況でA/AテストをしないままA/Bテストをしていると、本来は性能に差がないものであっても差があると結論づけてしまいそうです。特にA/Bテストが頻繁にされるようなプロダクトでKPIが改善する施策を作ることは難しいですが、この状況では簡単に統計的に有意な差が生まれてしまいます。そうすると、差がない施策を差があると解釈し、そこから仮説を考えて新しい施策をA/Bテストし、また差があるかどうかに関わらず有意な差が生まれるという悪夢のループが発生します。[6] あなたが直面しているA/Bテストも実はそうなったりしていませんか？うまくいったA/Bテストはほんとにうまくいったといい切れるでしょうか？

今回は上述の集計データからの軽い分析からみるに、原因はヘビーユーザの存在なのかもしれません。以降では、ヘビーユーザがいるようなケースを一般化しながら、A/AテストやA/Bテストをどのように評価していくかを考えていきます。

いろいろなクリック率と分散推定

ひとまず今私たちが考えたい問題設定を改めて整理してみます。

表記
- ユーザ i in
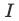
- インプレッション j in
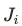
- ユーザiに与えられる割り当て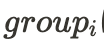in {“treatment”, “contol”}
  - 本来はA/Bテスト・A/Aテストにおいて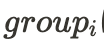は”treatment”・”contol”の2値からランダムに1つを引く確率変数ですが、ここでは実験開始時点で既に与えられた決定的な値とします。
  - 簡略化のために、変数の添字として”treatment”を意味する”t”や”contol”を意味する”c”を今後用います。
各々の群ではユーザiがインプレッションjで次の様にベルヌーイ分布から値をひきます.
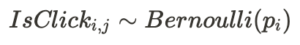
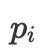- はユーザiに与えられたクリック率を表します。この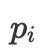がどのように決まるかは問題設定によって異なりますが、今回はA/Aテストを考えたいので、これもまた一様にランダムに定まるとします。
統計量(KPI):
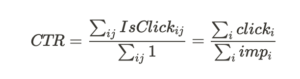
- 説明の簡略化のためにユーザiごとに集計したクリック数やインプレッション数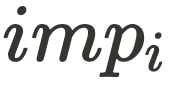という表記を導入しています
仮説検定の仮説
- トリートメント群とコントロール群それぞれのCTRが等しいかどうか

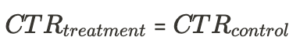
こうして改めて問題設定を文字に起こすと、今回のような分析事例は「分析単位と実験単位が異なる」ケースとして一般化することができます。A/Aテストではサンプルをランダムに2群に割り当てるわけですが、[2]に書いたとおり、その際の割り当て単位は多くの場合ユーザになります。一方で、集計で用いるCTRはインプレッションを単位として計算されます。同じユーザに対して複数回インプレッションがあることは極めてよくあるケースであることを考えると、インプレッションを単位としたA/BテストやA/Aテストデータにはそれぞれの群内に同一ユーザのデータが多数存在することになります。

同一ユーザは比較的似た行動をすると考えられるため、ナイーブにCTRを集計して分析をすることは時に議論をミスリードさせることがあります。前の節で図示したように、ヘビーユーザの挙動とA/Aテストのパフォーマンスの間にはどうやら関係があるようです。例えばそれは、CTRの分散の推定において重要な課題として浮き上がってきます。そもそも我々が何気なく用いているCTRという値はユーザの行動変数から構成される統計量なわけです。その時に「インプレッションベースのログデータからナイーブに分散を計算する」といったような推定量が果たして適切なものかどうかは必ずしも明らかではありません。そして、のちほどシミュレートしますが、このような状況が分散の推定量を0方向にバイアスさせてしまっているようです。

前節で記述したA/Aテストの失敗の原因も、実のところまさにこのナイーブな分散の計算によるものでした。分散が小さくなってしまうならばトリートメントとコントロール群の間に僅かの差しかない場合であっても、その差を統計的に有意だとしてしまうことも多くなってしまいます。前節で描いたようにA/Aテストが失敗してしまう背景にはこのような事象があります[7]。

A/Bテストについての良書Trustworthy本やDeng, Knoblich & Lu(2018)ではこのような事例における対処法をいくつか紹介してくれています。ここで列挙してしまえば、

ユーザベースCTRに直す
デルタメソッドの適用

などのテクニックです。本稿ではそれらに加えて、

クラスターロバスト分散推定の利用

も検討しています。以降ではこれらを詳細に見ていきましょう。

シミュレーションデータの組成

以降ではシミュレーションデータを作成し、そのデータに対する各手法の挙動を確認してみます。nをユーザ数とし、ユーザiがトリートメント群/コントロール群のどちらかに所属するかはランダムに定まるとします。そして、ユーザiのclick率は一様分布に従うとします。ただし、コントロール群のユーザのクリック率は0から1-δの値をとる一様分布から生成され、トリートメント群のユーザのクリック率はやはり0から1-δの値をとる一様分布から生成された値にδだけ足した値とします。そして、各々のユーザのインプレッション回数は1回から1000回までの範囲でランダムに定まるとします。

以上の設定に基づいて、次の様にシミュレーションデータを組成します。同時に本稿で用いるライブラリなどをインポートしておきます。

import hashlib
import string
from functools import reduce

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from scipy import stats
from tqdm import tqdm

ALPHABET = np.array(list(string.ascii_lowercase + ' '))

def gen_simulated_data(n: int, delta: float, seed: int=1) -> pd.DataFrame:
    np.random.seed(seed=seed)
    assignment = np.random.choice([0, 1], size=n)
    num_visits = np.random.randint(low=1, high=1000, size=n)
    ctr = np.random.uniform(0, 1 - delta, size=n)
    ctr[assignment==1] += delta
    uid_vec = np.repeat(range(n), num_visits, axis=0)
    treatment_vec = np.repeat(assignment, num_visits, axis=0)
    ctr_vec = np.repeat(ctr, num_visits, axis=0)
    clicks_vec = reduce(lambda a, b: np.r_[a, b], [np.random.choice([0, 1], size=num_visits[i], p=[1 - ctr[i], ctr[i]]) for i in np.arange(n)])
    df = (
        pd.DataFrame(
          np.c_[uid_vec, treatment_vec, clicks_vec], 
          columns=['uid', 'is_treatment', 'is_click']
        )
        .astype({'uid': int, 'is_treatment': int, 'is_click': int})
    )
    return df

今回はA/Aテストを行うような状況を考えたいのでとして、例えば次の様にデータが生成されます。

df = gen_simulated_data(n=300, delta=0, seed=10)
df

uid/is_treatment/is_clickの3つのカラムがありますが、それぞれユーザID/「トリートメント群か否か」/「クリックがあったかどうか」を表します。レコード単位はインプレッションです。このデータは実際のログデータを模したものになっているはずです。

インプレッションベースCTRを用いた分析とその失敗

各手法を見ていく前に、インプレッションベースCTRを用いた分析のケースを示します。インプレッションベースCTRでA/Bテスト・A/Aテストをする場合には、クリック有無の平均の差の検定を行います。

def get_test_result_plain_from_simulated_df(dfx: pd.DataFrame, column_treatment='is_treatment', column_click='is_click'):
    mean_treated, var_treated, n_treated = dfx[dfx[column_treatment] == 1][column_click].mean(), dfx[dfx[column_treatment] == 1][column_click].std(), dfx[dfx[column_treatment] == 1][column_click].count()
    mean_control, var_control, n_control = dfx[dfx[column_treatment] == 0][column_click].mean(), dfx[dfx[column_treatment] == 0][column_click].std(), dfx[dfx[column_treatment] == 0][column_click].count()
    return stats.ttest_ind_from_stats(mean_treated, var_treated, n_treated, mean_control, var_control, n_control, equal_var=False)

result_impression = get_test_result_plain_from_simulated_df(dfx=df, column_treatment='is_treatment', column_click='is_click')
print(f"""
AAテスト結果(リクエストベース)：
stat: {result_impression.statistic:.3f}
pvalue: {result_impression.pvalue:.3f}
""")

AAテスト結果(リクエストベース)：
stat: 5.228
pvalue: 0.000

インプレッションベースCTRを用いて仮説検定を行った結果、A/Aテストは失敗してしまいました。すなわち本来A/Aテストにおいて「トリートメント群か否か」は単にユーザごとにランダムに割り当てただけの値であるのにもかかわらず、その2つの群間の差のp値は1%以下で統計的に有意です。これは前節で示した実例におけるA/Aテストが失敗してしまった結果とも整合的です。各割当での平均値はそれぞれ約0.484, 0.498で、比にすると約2.9%ほど“改善“しているように見えます。この差が大きいかどうかは事業の状況や施策のコストによりそうですが、事業的に意味のある差だとするケースも十分にありそうです。A/Bテストのレポートとしては、「今回の介入はクリック率を2.9%改善させて、統計的にも有意な差だったので100%適用する」などとなってしまいそうです。どうやら、この統計量を用いたままA/Bテストを行ってしまうと、正確に評価できない蓋然性は高そうです。なにしろ、2群に同じ介入を行ってもその2群の差は有意であるとしてしまうような統計量なのですから。

ユーザベースCTRに直す

まず最初に考えてみたいのは、計算するCTRの定義を変えて”ユーザベースCTR”を計算するというものです（逆にここまでナイーブにCTRと呼んできたものを、ここからは”インプレッションベースCTR”と呼びましょう）。ユーザベースCTRはその名の通り、CTRの単位をユーザベースに直したものです。すなわち、ユーザごとにCTRを計算しさらにその平均を取ることで得られる値です。数式で書くならば、

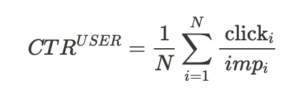
といった様に定義されます(は0より大きいとします)。このユーザベースCTRは分析単位と実験単位が一緒のため、上述の様なケースでは上手に分散を推定することができます。

では、その手法の挙動について実際に確かめてみましょう。ユーザベースCTRを出してみます。次のように非常に簡単にユーザごとのCTRやその分散は計算することができます。

df_groupby = df.groupby('uid').mean()
print(f"""
ユーザベースCTR：平均 {df_groupby['is_click'].mean():.3f}, 分散 {df_groupby['is_click'].var():.3f}
""")

ユーザベースCTR：平均 0.484, 分散 0.082

A/Aテストを実際にやってみます。比較のために、インプレッションベースCTRを用いたA/Aテストも見てます。ここでは、上述のログデータやログデータのユーザ平均データを用いて、平均の差の検定を行っております。

result_user = get_test_result_plain_from_simulated_df(dfx=df_groupby, column_treatment='is_treatment', column_click='is_click')
result_impression = get_test_result_plain_from_simulated_df(dfx=df, column_treatment='is_treatment', column_click='is_click')
print(f"""
AAテスト結果(リクエストベース)：
stat: {result_impression.statistic:.3f}
pvalue: {result_impression.pvalue:.3f}

AAテスト結果(ユーザベース)：
stat: {result_user.statistic:.3f}
pvalue: {result_user.pvalue:.3f}
""")

AAテスト結果(リクエストベース)：
stat: 5.228
pvalue: 0.000

AAテスト結果(ユーザベース)：
stat: 0.454
pvalue: 0.650

ユーザベースCTRを用いた分析はA/Aテストの意図通りの挙動をしています。すなわち、インプレッションベースCTRのA/Aテストにおけるp値は1%以下ですが、ユーザベースCTRのA/Aテストにおけるp値は0.650と大きくなっており、当然統計的に有意ではありません。これは決してp-hackingなどではないことを後ほど示しますが、このようにユーザベースCTRではユーザ固有の効果をうまく排除して分散が大きく推定されていることがわかるかと思います。

デルタメソッドによる漸近分散の導出

Deng et al.(2018)ではA/Bテストにおいて分析単位と実験単位が異なるようなときにビジネスKPI（ここではインプレッションベースCTR）の分散を推定する方法として、デルタメソッドを用いる方法を紹介しています。詳細な式展開は論文を読んでいただくとして、インプレッションベースCTRの分散は次の様に近似することができます。

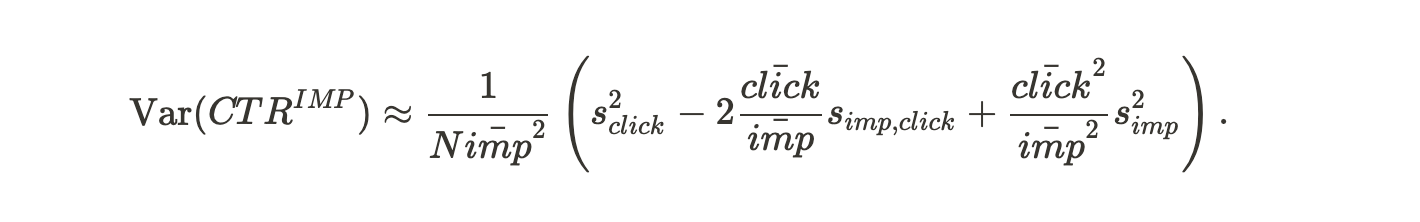
ただしNはユーザ数、はクリック数の分散、はインプレッション数の分散、はインプレッション数とクリック数の共分散、はユーザごとのインプレッション数の平均、はユーザごとのクリック数の平均を表します。ユーザごとのインプレッションデータがあればこの手法は適用することができます。

A/Aテストの仮説検定プロセスにおいて、上記近似式によって導出した分散を用いてみましょう。上記シミュレーションデータのテーブル構造を前提にして次の様にA/Aテストを実行します。仮説検定としては変わらず平均の差の検定をしています。[8]

def var_delta(data, column, label, ddof=1):
    grouped = data.groupby(column)
    s = grouped[label].sum()
    n = grouped[label].count()
    mean_s = s.mean()
    mean_n = n.mean()
    covar_mat = np.cov(s, n, ddof=ddof)
    var_s = covar_mat[0][0]
    var_n = covar_mat[1][1]
    covar_sn = covar_mat[0][1]
    k = len(s)
    return (1.0 / (k * (mean_n ** 2))) * (var_s - 2 * (mean_s / mean_n) * covar_sn + ((mean_s ** 2) / (mean_n ** 2)) * var_n), k

def get_test_result_delta_from_simulated_df(dfx: pd.DataFrame, column_treatment='is_treatment', column_click='is_click', column_uid = 'uid'):
    mean_treated = dfx[dfx[column_treatment] == 1][column_click].mean()
    mean_control = dfx[dfx[column_treatment] == 0][column_click].mean()
    var_treated, n_treated = var_delta(data=dfx[dfx[column_treatment] == 1], column=column_uid, label=column_click)
    var_control, n_control = var_delta(data=dfx[dfx[column_treatment] == 0], column=column_uid, label=column_click)
    return stats.ttest_ind_from_stats(
        mean_treated, np.sqrt(var_treated * n_treated), n_treated, 
        mean_control, np.sqrt(var_control * n_control), n_control, 
        equal_var=False
    )

result_impression = get_test_result_plain_from_simulated_df(dfx=df, column_treatment='is_treatment', column_click='is_click')
result_delta = get_test_result_delta_from_simulated_df(dfx=df, column_treatment='is_treatment', column_click='is_click', column_uid = 'uid')
print(f"""
AAテスト結果(リクエストベース)：
stat: {result_impression.statistic:.3f}
pvalue: {result_impression.pvalue:.3f}

AAテスト結果(デルタメソッド)：
stat: {result_delta.statistic:.3f}
pvalue: {result_delta.pvalue:.3f}
""")

AAテスト結果(リクエストベース)：
stat: 5.228
pvalue: 0.000

AAテスト結果(デルタメソッド)：
stat: 0.344
pvalue: 0.731

デルタメソッドを用いた分析はA/Aテストの意図通りの挙動をしています。すなわち、インプレッションベースCTRのA/Aテストにおけるp値は1% 以下ですが、分散をデルタメソッドで計算したp値は0.731と大きくなっており、当然統計的に有意ではありません。このようにデルタメソッドを用いると分散が大きく推定されていることがわかるかと思います。

（追記）

社内の有識者から「そもそも元々の確率変数が従う分布はベルヌーイ分布であり、また今回のKPIであるCTRという値もそのベルヌーイ分布のパラメータの推定量では。そうであれば、ベルヌーイ分布の平均が集計によってわかるのだから、そこから分散も構成できるはず。そうであれば、その平均や分散からなんとか検定統計量を構成できないか(わざわざデルタメソッドを用いる必要はないのでは)」という指摘を受けております。本稿の公開時期などから私たちの間でまだ検討が足りていないのですが、今後この方向性でも考えてみたいと思います。

クラスターロバスト標準誤差の利用

実験単位と分析単位が異なる時に得られるサンプルの分散が均一でないというのが問題なのでした。その際に使える手法として、回帰分析の際にクラスターロバスト標準誤差を用いるというのも有用なアイディアになりえます。クラスターロバスト標準誤差とはその名の通りクラスター内での誤差項間の相関を許した標準誤差を指し、パネルデータ分析などで頻繁に用いられます。計量経済学を学んだ人にとっては、良さげに思えた回帰結果の統計的な有意性を無慈悲に無に返すおなじみの標準誤差です。ここでは各ユーザがクラスタを表し、同一ユーザ内での誤差項の相関を許すというわけです。

クラスターロバスト標準誤差を用いて分析をしてみた結果が次の通りです。ここでは検定として、回帰分析の係数についてのt検定を行っております。

import statsmodels.api as sm
import numpy as np

def get_test_result_cluster_robust_from_simulated_df(dfx: pd.DataFrame, column_treatment='is_treatment', column_click='is_click', column_uid = 'uid'):
    model = sm.OLS(df[column_click], sm.add_constant(df[column_treatment]))
    result = model.fit()
    result_robust = result.get_robustcov_results(cov_type='cluster', groups=df[column_uid].astype(int))
    return result_robust

result_robust = get_test_result_cluster_robust_from_simulated_df(dfx=df, column_treatment='is_treatment', column_click='is_click', column_uid = 'uid')
print(f"""
AAテスト結果(リクエストベース)：
stat: {result_impression.statistic:.3f}
pvalue: {result_impression.pvalue:.3f}

AAテスト結果(クラスターロバスト)：
stat: {result_robust.summary2().tables[1].loc['is_treatment', 't']:.3f}
pvalue: {result_robust.summary2().tables[1].loc['is_treatment', 'P>|t|']:.3f}
""")

AAテスト結果(リクエストベース)：
stat: 5.228
pvalue: 0.000

AAテスト結果(クラスターロバスト)：
stat: 0.345
pvalue: 0.731

クラスターロバスト標準誤差を用いた分析もやはりA/Aテストの意図通りの挙動をしています。すなわち、インプレッションベースCTRのA/Aテストにおけるp値は1%以下ですが、クラスターロバスト標準誤差を用いたp値は0.731と大きくなっており、当然統計的に有意ではありません。このようにクラスターロバスト標準誤差を用いると分散が大きく推定されていることがわかるかと思います。

（追記）

この0.731というp値はデルタメソッドによる分散の推定を行った時に得られるp値と等しいことに注意をしてください。デルタメソッドによって推定された分散とクラスターロバスト標準誤差は実は同じ推定量の様です。筆者は論文をしっかり読んだわけではないのでその存在だけ紹介させていただきますが、Deng, Lu and Win(2021)ではまさにその議論を行っているようです（この論文はまさにこの原稿を書いている時に見つけました。。。笑）。

A/Aのreplay

ここまでユーザごとに割り当てを行うような実験での分析テクニックを紹介し、実際にA/Aテストにおけるp値が大きくなっているのを観察してきました。しかし実のところ、たまたまそういった乱数を引いただけなのかもしれず、これだけではA/Aテストとしては十分ではありません。Trustworthy本にも紹介されていますが、A/Aテストを繰り返して得られるp値が0.05未満で統計的有意になる確率は大まかに5%でないといけません。A/Aテストを大量に実行できればいいのですが、実際の本番環境においては難しいことも多いはずです。

そういった際に用いる手法としてTrustworthy本ではA/Aテストのreplayが紹介されています。A/Aの割当を（ハッシュのソルトを変えることなどで）繰り返し変えることでA/Aテストを複数回シミュレーションするのです。この手法はシステムのバグなどに気を配ったものではありませんが、A/Bテストの評価指標の計算方法が適切かどうかは確認することができます。例えば、割当を変えるシミュレートを1000回ほど行い、その度に得られるp値の分布をプロットしてみることでA/Aテストの設計が正しいかどうかを目視することができます。すなわち、正しくA/Aテストが設計できていれば、その分布は一様分布に近しいものであるはずです。必要であればコルモゴロフ-スミルノフ検定などの適合度検定を用いても良いでしょう。このようにして、A/Aテストを実運用で繰り返さなくともA/Aテストの結果をシミュレートすることができるのです。

それではここまで紹介してきた手法を実際にシミュレートしてみましょう。500回ほどランダムな割り当てを行い、その度にそれぞれの手法でp値を計算してみます。

def assign_treatment_randomly(uid: int, salt: str):
    return int(hashlib.sha256(f"{salt}user{uid}".encode()).hexdigest(), 16) % 2

def assign_treatment_by_uid(dfx: pd.DataFrame, seed: int = 1, column_name = 'is_treatment_in_aa'):
    np.random.seed(seed=seed)
    salt = ''.join(np.random.choice(ALPHABET, size=10))
    dfx[column_name] = np.vectorize(assign_treatment_randomly, otypes=[float])(uid=dfx['uid'].astype(int), salt = salt)

replays = []
for i in tqdm(range(500)):
    assign_treatment_by_uid(df, seed=i, column_name = 'is_treatment_in_aa')
    result_user = get_test_result_plain_from_simulated_df(dfx=df.groupby('uid').mean(), column_treatment='is_treatment_in_aa', column_click='is_click')
    result_impression = get_test_result_plain_from_simulated_df(dfx=df, column_treatment='is_treatment_in_aa', column_click='is_click')
    result_delta = get_test_result_delta_from_simulated_df(dfx=df, column_treatment='is_treatment_in_aa', column_click='is_click', column_uid = 'uid')
    result_robust = get_test_result_cluster_robust_from_simulated_df(dfx=df, column_treatment='is_treatment_in_aa', column_click='is_click', column_uid = 'uid')
    replays.append([
        i, result_impression.pvalue, result_user.pvalue, result_delta.pvalue, result_robust.summary2().tables[1].loc['is_treatment_in_aa', 'P>|t|']
    ])
replays_df = pd.DataFrame(replays, columns=['i', 'impression', 'user', 'delta', 'robust'])

結果を可視化してみます。500回のreplayから得られるp値のヒストグラムを描いてみました。

column_to_title = {
    'impression': 'CTR(impression base)', 'user': 'CTR(user base)', 'delta': 'Delta Method', 'robust': 'Cluster Robust Std.'
}
fig, axs = plt.subplots(1, 4, figsize=(17, 4))
for i, column in enumerate(['impression', 'user', 'delta', 'robust']):
    ax = axs[i]
    ax.hist(replays_df[column])
    [spin.set_visible(False) for spin in list(ax.spines.values())]
    ax.spines['bottom'].set_visible(True)
    ax.spines['left'].set_visible(True)
    ax.set_facecolor("none")
    ax.set_xlabel('pvalue')
    ax.set_title(column_to_title[column])
plt.show()

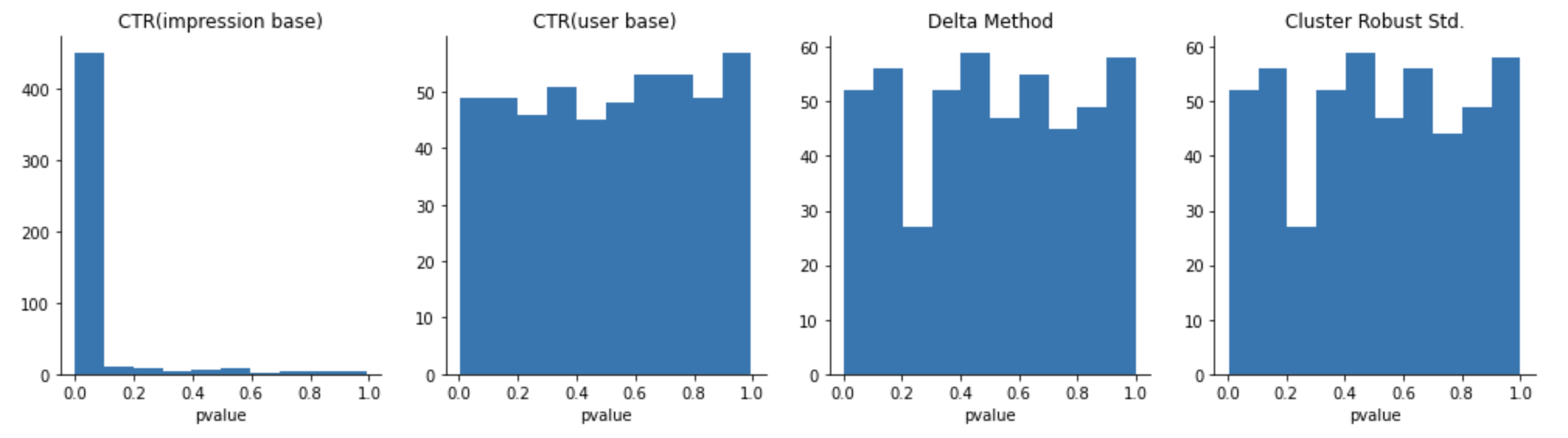
この結果から分かる通り、インプレッションベースの場合には得られたp値はまったく一様分布的ではなく、0付近に偏っていることを見てとることができます。すなわち、割り当てがユーザベースで行われている時、インプレッションベースのA/Aテストは失敗してしまう確率は非常に高くなります。その一方で、本稿で紹介してきた手法はいずれも比較的一様分布的であることを見てとることができるかと思います。念のため適合度検定をしておきましょう。

for column in ['impression', 'user', 'delta', 'robust']:
    result = stats.kstest(replays_df[column], stats.uniform.cdf)
    print(f"""
    適合度検定: {column_to_title[column]}
    stat: {result.statistic:.3f}
    pvalue: {result.pvalue:.3f}
    """)

適合度検定: CTR(impression base)
stat: 0.848
pvalue: 0.000

適合度検定: CTR(user base)
stat: 0.028
pvalue: 0.815

適合度検定: Delta Method
stat: 0.035
pvalue: 0.594

適合度検定: Cluster Robust Std.
stat: 0.034
pvalue: 0.630

インプレッションベースCTRにおける適合度検定ではp値は1%以下であり、replayから得られる個々のp値が従う分布は一様分布と大きく異なることが示唆されます。一方で、ユーザベースCTR/デルタメソッド/クラスターロバスト標準誤差における適合度検定ではp値は10%を超えて有意ではありません。すなわち、replayから得られる個々のp値が従う分布は一様分布と似ていることが示唆されます。このようにインプレッションベースCTRをユーザベースCTRに直したり、そのままインプレッションベースCTRを使うにせよその統計量に応じた分散を推定してあげることがA/Bテストの遂行において有用であることがわかりました。

実務でどうするか？

前節で、インプレッションベースCTRではなくユーザベースCTRを用いたり、インプレッションベースCTRの分散推定にデルタメソッド、クラスターロバスト標準誤差を利用すると、A/Aテストが成功することがわかりました。この節では、実務的な事情を考慮してどういう指標を使うべきか議論します。

ユーザベースCTRの性質

性質が良いように思われるユーザベースCTRは、インプレッションベースCTRとどのような関係にあるのでしょうか。簡単な式展開でユーザベースCTRの性質を明らかにすることができます。ユーザベースCTRは、

と変形することができます。ここから、全ユーザが同じM回インプレッションしたとすると、ユーザベースCTRとインプレッションベースCTRが一致することがわかります。

具体的な数値例で説明します。3人のユーザに対して、以下の配信結果が得られたとします。

USER	click	imp
A	1	3
B	1	5
C	5	10

インプレッションベースCTRでは、分子分母をそれぞれのユーザで足し上げるので、(1 + 1 + 5)/(3 + 5 + 10) = 7/18となります。ユーザベースCTRではそれぞれのCTRを足して平均するので1/3(1/3 + 1/5 + 5/10) = 1/3(50/150 + 30/150 + 75/150) = (50 + 30 + 75) / (150 + 150 + 150) = 155/450となります。これは、M=450回として通分する( = 全員が同じM回インプレッションする）ときに分子分母をそれぞれ足し上げるインプレッションベースCTRの計算方法でユーザベースCTRを求められます。したがって、ユーザベースCTRは全員が同じM回インプレッションしたときのインプレッションベースCTRの値と解釈できるのではないかということです。

さらに、クリックの変動が各CTRに与える影響を見るために、各CTRをあるユーザiのクリックで偏微分すると、

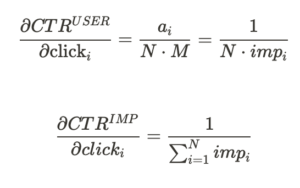
という関係性を見出すことができます。これらはそれぞれ、

ユーザベースCTRでは、インプレッションが大きいヘビーユーザはクリックの係数である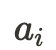が相対的に小さくなり、インプレッションが小さいユーザに比べてCTRに与える影響が小さくなる

⇨ インプレッションが多い外れ値ユーザに対して頑健

インプレッションベースCTRでは、クリックのCTRに対する影響が全インプレッションで同じ

⇨ インプレッションが多い外れ値ユーザの影響を受けやすくなる

という性質を意味します。

ユーザベースCTRの欠点

上述のように、ユーザベースCTRはインプレッションが多いヘビーユーザとインプレッションが少ないライトユーザを等しく扱います。これは、売上などのビジネス指標への直接的なインパクトを評価したい場合には不適なことがあります。[9]特に、インプレッションの多さとビジネス的なユーザの価値が大きく関係している場合は注意が必要です。Dynalystの場合、1つの広告キャンペーンの対象にしかならないユーザより、多くのキャンペーンの対象になるユーザ（≒ たくさんのアプリをインストールしているユーザ）の体験を改善したほうが、（短期的な）売上に寄与します。ECサイトの場合は、水しか買わないユーザより生活必需品から家電やホビー用品までたくさん買うユーザの体験を改善したほうが、売上に寄与します。それらを議論した結果、Dynalystでは見るべきKPIはインプレッションベースCTRとすることになりました。

デルタメソッドの欠点と結局どうしているか

インプレッションベースCTRをKPIとするならば、前節で説明したとおりデルタメソッド等で分散を導出をする必要があります。それを、A/Bテストの結果を可視化・評価するダッシュボード上で行うぶんには問題ありません。しかし、集計範囲や粒度を変えたり、セグメントごとに分析するようなEDAフェーズでは、デルタメソッドによる分散の導出を毎回行うのはかなりめんどうです。 Dynalystでは、厳密な評価と分析コストのトレードオフを考慮して、

EDAフェーズでは分散が過小に推定されるのを理解した上で、インプレッションベースCTRとインプレッションベースの分散を用いる
最終的な施策の是非に関する意思決定は、インプレッションベースCTRとデルタメソッドによって導出された分散を用いて評価を行う

としています。

まとめ

このブログでは同じ介入を比較するA/Aテストですら統計的に有意な差が出てしまう状況が存在することを説明しました。それを無視してA/Bテストを行えば”うまく”いってしまう（=統計的に有意な差が生まれる）のですが、それは幻想に過ぎず、A/Bテストの指標の設計に失敗しているだけである可能性を指摘しました。この問題の対処法としてユーザベースCTR、デルタメソッドの活用、クラスターロバスト標準誤差を紹介しました。しかし、それらの手法は実務的に運用する上では一長一短です。暫定的な運用方針は定めていますが、まだ正解はわからないので、日々の分析の中でアップデートしていきたいと考えています。

注釈

[1] Kohavi, Tang & Xu(2020)のことをここではTrustworthy本と呼んでます。

[2] ユーザ単位で実験の割当を行うのは、あるユーザがアルゴリズムAとアルゴリズムBのどちらかの広告にしか接触しないようにするためです。仮にインプレッション[3]を単位にして割当を行った場合、同じユーザの別のインプレッションにおいて異なる割当が発生する可能性があります。ユーザへの長期的な影響を見たい場合など、アルゴリズムAによる広告を見たユーザが同時期にアルゴリズムBの広告を見ていることを許容できないケースは多いでしょう。

[3] インプレッション: 広告用語で、ユーザのアプリ / ブラウザ画面に広告が表示されることを指します。

[4] ウェブ業界ではよくある設定ですが、各レコードは、インプレッションを試行、クリックを成功とするベルヌーイ分布からサンプリングされたものと考えています。その設定のもとで、ベルヌーイ分布の期待値（=クリック率）がA群とA’群が同じであるという仮説に対してt検定をしています。この設定がやや不適切であることやその対処法については、次の節で述べます。

[5] botと思われるユーザについては、ビジネスルールで判別し集計から除外しています。

[6] 真の平均に差はないはずなのに、統計的な有意差が生まれてしまう今回のケースでは、Trustworthy本に載っているようなpractically siginificance（実務的に有意）を考慮すれば、一部回避できる話でもあります。

[7] もしくは、上述の様な問題設定においてログデータを分析をするという文脈では、各々のサンプル間の独立性に注目しても良いかもしれません。は各ユーザに与えられている値であるため、そのユーザのレコード間ではサンプル（例えばクリックの有無）は独立になっておりません。このような時に、やはり適当にログデータ全体の分散を計算することが適切かどうかは自明ではありません。

[8] ただし上記データで求まるのはという標本に対して1つに定まる統計量の分散です。平均の差の検定を既存パッケージなどでお手軽に行うために、ここではナイーブな方法で平均の差の検定を行っています。

[9] 施策の目的によって、適切なKPIは変わります。たとえば、ライトユーザ含めユーザ全体の体験を改善することが目的であればユーザベースCTRが適切な指標になりえます。

参考文献

Deng, A., Knoblich, U., & Lu, J. (2018, July). Applying the Delta method in metric analytics: A practical guide with novel ideas. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (pp. 233-242).

Deng, A., Lu, J., & Qin, W. (2021). The equivalence of the Delta method and the cluster-robust variance estimator for the analysis of clustered randomized experiments. arXiv preprint arXiv:2105.14705.

Kohavi, R., Tang, D., & Xu, Y. (2020). Trustworthy online controlled experiments: A practical guide to a/b testing. Cambridge University Press.

タップル iOSにおけるFeature Module開発の導入と運用

snowflakeでのクエリのパフォーマンス改善に向けた取り組み

なぜあなたのA/Bテストはうまくいくのか？A/Bテストの分析で注意すること

概要