本記事は、CyberAgent Advent Calendar 2022 19日目の記事です。

目次

1. はじめに
2. 問題設定
3. 協調フィルタリングのための線形モデル
   • iALS
   • EASE
4. 関連する非線形モデル
5. 実務活用
6. おわりに

はじめに

メディア DSC所属の機械学習エンジニアで、タップルの推薦システムを担当している橋爪 (@runnlp)です。

最近、推薦システムを触り始めました。推薦手法は、協調フィルタリング、コンテンツベース、ハイブリッドなど様々ですが、今回は昔から今に至るまで長く使われている協調フィルタリングについてです。

協調フィルタリングではDeep系のモデルがたくさん出る中で、RecSys2022で発表された論文では10年以上前から使用されている線形モデル(iALS)がDeep系のモデルに匹敵する結果であると報告されており興味深いです。また、推薦システムを開発するにあたって、問題設定やモデリングを正しく理解して進めるためにも計算コストや実行時間を抑えるためにもシンプルな線形手法から始めたい場合もあると思います。

このブログでは線形モデルで今でも優れた精度であるiALSとEASEを説明します。その後、紹介する線形モデルと通ずる部分があるため、最近のDeep系の手法の紹介もします。システムについても少し触れます。

導出や解釈を丁寧に書いているため長いブログになっていますが、読んでいただけると嬉しいです。

問題設定

implicit feedback

学習データとして用いるimplicit feedbackについて説明します。これはユーザ集合\(U\)とアイテム集合\(I\)があったときに、ユーザ\(u\in{U}\)がアイテム\(i\in{I}\)に対する行動履歴を表すデータで、以下のようなスパース行列のことです。
$$X\in\mathbb{R}^{|U|\times|I|}$$

基本的にバイナリでユーザがアイテムに何らかの行動をしている場合には1,そうではない場合には0が入っています。ここでの行動というのは、動画配信サイトやECサイトの場合はクリック、マッチングアプリの場合にはいいねなどが考えられます。\(|U|=5\), \(|I|=4\), の例です。2人目のユーザは1つ目のアイテムだけをクリックしていることがわかります。

また、実世界のデータはimplicit feedbackが多いですが、扱いづらい点としては、negative feedbackが観測されない(positive-only setting)があります。これによってユーザが接触してかつクリックなどをしたアイテムに対するpositive feedbackしか得ることができません。このことから、ユーザがどのアイテムを好まなかったかを推測することが困難です。例えば、ある動画をクリックしなかったユーザは嫌いだったから観なかったのか、単純にまだ観てないだけなのかはわかりません。

何を解く問題なのか

上記のデータ\(X\)を用いて、ユーザ\(u\in{U}\)とアイテムの集合\(I\) (事前に絞り込まれている場合には集合\(I\)の部分集合)を用いて、アイテムをユーザ\(u\)の好み順に並べ替えるランキングの問題になります。より好みのアイテムを上位にすることが目的になるので、top-N件にどれだけ正解データが含まれるかを用いた指標 (e.g., Precision@N, Recall@N)が評価で使われることが多いです。このようなタスクはtop-N item recommendationと呼ばれています。

 

協調フィルタリングのための線形モデル

このセクションでは精度もDeep系に匹敵すると報告されている線形モデルであるiALSとEASEに重点を置いて紹介します。iALSは10年以上前からあるにも関わらずRecSys2022の最新の論文でDeep系に匹敵すると報告されています。EASEは、2019年に発表されており閉形式解があり勾配法のような繰り返しの更新がいらないことやモデルの構造が簡単なことが特徴的です。またMSDと呼ばれるデータセットでは最も性能が良いことが報告されています。

iALS

iALSは、行列分解を用いた手法です。推薦システムのベースラインとしてよく利用されています。ここでは、2008年に発表されたiALSと、iALSのチューニングなどをして再検証することで精度が最新のモデルにも匹敵することが示された2022年の論文について説明します。

※ iALSの元論文ではモデルの名前が明示されていませんが、このブログでは2022年の論文に合わせてiALSと呼びます。他の論文ではWRMF、WMF、WALSなどと表記されていることもあります。

モデル定義

行列分解の手法では、feedback行列\(X\)をユーザの因子ベクトル\(P\)とアイテムの因子ベクトル\(Q\)に分解して得たベクトルを用いて推薦を行います。ユーザの因子ベクトルとアイテムの因子ベクトルがわかれば未観測のユーザ-アイテムペアに対してもスコアを出すことができます。

$$X\approx P\cdot Q^\top$$

ユーザ\(u\in U\)が与えられた時に、アイテム\(i\in I\)の予測スコアは、以下の式で定義されます。

$$\hat X_{ui}=\langle p_u, q_i \rangle$$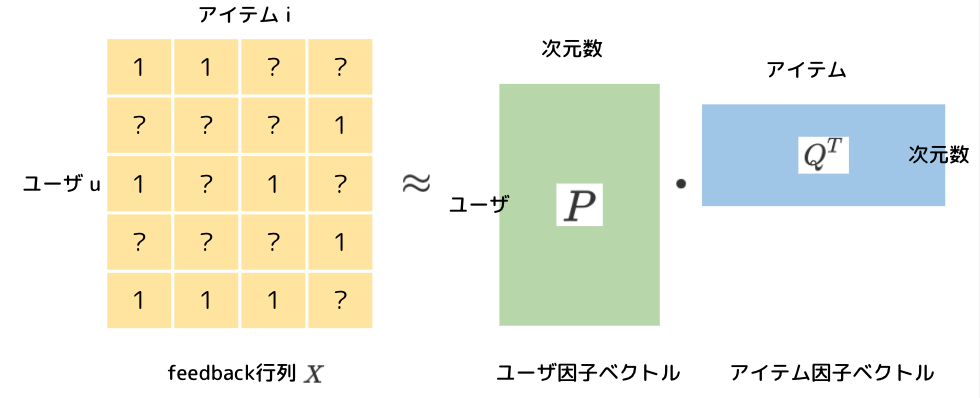

目的関数

\({(u,i)}\in S\)が\(X_{u,i}=1\)、すなわちユーザ\(u\)がアイテム\(i\)に対して行動をしたことを表すとすると、目的関数は以下のように表すことができます。
$$L(P,Q) = \sum_{{(u,i)}\in S}\left(\langle p_u, q_i\rangle-1\right)^2+\alpha_{0}\sum_{u\in U}\sum_{i\in I}\langle p_u, q_i \rangle^2+\lambda\left(\sum_{u\in U}\|p_u\|_2^2 +\sum_{i\in I}\|q_i\|_2^2\right)$$

第1項では\(X_{u,i}=1\)であるユーザ-アイテムペアに対する平均二乗誤差 (mean squared error; MSE)です。第2項はimplicit feedbackのための項で、全体のスコアを小さくするように導入されています。ここでは\(\alpha_0\)によって未観測のデータ（\(X_{u,i}=1\)）と観測済みのデータ(\(X_{u,i}=0\))で、学習の重要度に差をつけることができます。また第3項はL2正則化になります。

最適化

Alternating Least Squares (交互最適化)では、アイテムとユーザをそれぞれ固定して交互に最適化を行います。そのためアイテムを固定したときのユーザの更新式は、以下のように算出することができます。

$$\begin{eqnarray}\\
\frac{\partial}{\partial p_u}L(P,Q) &=& \frac{\partial}{\partial p_u}\left(\sum_{{(u,i)}\in S}(\langle p_u, q_i\rangle-1)^2+\alpha_{0}\sum_{u\in U}\sum_{i\in I}\langle p_u, q_i \rangle^2+\lambda(\sum_{u\in U}\|p_u|_2^2 +\sum_{i\in I}\|q_i\|_2^2)\right)\\
&=&2\sum_{{(u,i)}\in S}p_u q_i q_i^\top -2\sum_{{(u,i)}\in S}q_i+2\alpha_{0}\sum_{i\in I}p_u q_i q_i^\top +2\lambda p_u
\end{eqnarray}$$

上の勾配を0として、\(p_u\)について整理すると、
$$p_u = \left(\sum_{{(u,i)}\in S}q_i q_i^\top+\alpha_{0}\sum_{i\in I}q_i q_i^\top +\lambda I\right)^{-1}\sum_{{(u,i)}\in S}q_i$$

ユーザを固定した場合のアイテムの更新式も同様に
$$q_i = \left(\sum_{{(u,i)}\in S}p_u p_u^\top +\alpha_{0}\sum_{u\in U}p_u p_u^\top +\lambda I\right)^{-1}\sum_{{(u,i)}\in S}p_u$$

このように\(P\) (あるいは\(Q\))を固定した場合の最適化は、単純な問題 (ユーザ\(p_u\)(あるいはアイテム\(q_i\))に独立)となるので、ユーザとアイテムに対して並列に計算することができるのもポイントです。この並列性によって、ユーザとアイテムがどれだけ増えても、コア数を増やせば無限に速くできます。

スケーラビリティ

iALSは計算効率が良くスケーラビリティの高い手法として知られています。ここで計算量とそれを抑えるために重要になる2つのポイントについて説明します。

ユーザの更新式について考えます。
$$p_u = \left(\sum_{{(u,i)}\in S}q_i q_i^\top +\alpha_{0}\sum_{i\in I}q_i q_i^\top  +\lambda I\right)^{-1}\sum_{{(u,i)}\in S}q_i$$

1: Feedback Sparsity
まずは逆行列の第1項について考えます。ユーザごとの計算量はユーザの平均feedback数を\(|S|/|U|\)で表せることを用いて、\(O(|S|/|U|d^2)\)となり、ユーザ全員分の計算量は\(O(|S|d^2)\)となります。
$$\sum_{{(u,i)}\in S}q_i q_i^\top $$

ここでFeedback Sparsityがあることが重要になります。Feedback Sparsityとは、\(S\) (feedbackがあるデータ)というのはユーザ-アイテムのペアの総数\(|U||I|\)の中でわずか一握りにすぎないということです。ペアの総数とfeedback数の関係は、\(|U||I|\gg|S|\)になるので許容できる量であることがわかります。

2: Gramian Trick
次に逆行列の第2項について考えます。ユーザ全体の計算量は、\(O(|U||I|d^2)\)となり、\(|U||I|\)が出てきてしまうため、現実的ではありません。
$$\alpha_{0}\sum_{i\in I}q_i q_i^\top $$

しかし、\(\sum_{i\in I}q_i q_i^T\)はユーザに非依存であるため、ユーザごとに計算する必要がなく、全体で1度計算してしまえば使い回すことができます。そのため計算量は\(O(|I|d^2)\)とすることができます。また、\(|I|<|S|\)であることから、この計算量は前述の\(O(|S|d^2)\)によって無視することができます。

(行列の積の計算量は\(O(d^3)\)、行列の和の計算量は\(O(d^2)\))

計算量
方程式を解く部分は、ユーザごとに\(O(d^3)\)より、全体で\(O(|U|d^3)\)。前述の計算と合わせると、ユーザベクトルの1回の更新にかかる計算量は\(O(|S|d^2+|U|d^3)\)なります。アイテムベクトルについても同様に考えることができるため、アイテムベクトルの1回の更新にかかる計算量は\(O(|S|d^2+|I|d^3)\)となります。それらを合わせて全パラメタの更新を1回やるときの計算量は、\(O(|S|d^2+(|U|+|I|)d^3)\)と算出することができます。

また、モデルサイズはアイテム数とユーザ数に対して線形であることや内積で計算できるので近似近傍探索アルゴリズムなどを用いてuserの上位n件に効率的に問い合わせることができることもスケーラビリティが高いと言われる要因です。

Matrix Factorizationとの違い

行列分解というと、Netflix PrizeというNetflix主催のアルゴリズムコンテストで登場した手法であるMatrix Factorizationがよく知られていると思います。このモデルはもともとはexplicit feedbackのデータに用いられる手法であるため、iALSではimplicit feedbackでも対応できるように目的関数が拡張されています。Matrix FactorizationとiALSの目的関数は以下です。Matrix factorizationはMSEの最小化だけを行なっているのに対して、iALSの第1項は観測したペアに関するMSEですが、第二項は観測項も含む全ペアに対する再構成行列のノルムを小さくするようにしており、MSEの最小化を目指していません。

Matrix Factorization
$$L(p,q) = \sum_{u\in U}\sum_{v\in V}(\langle p_u, q_i\rangle-x_{u,i})^2$$

iALS
$$L(p,q) = \sum_{{(u,i)}\in S}(\langle p_u, q_i\rangle-1)^2+\alpha_{0}\sum_{u\in U}\sum_{i\in I}\langle p_u, q_i \rangle^2+\lambda\left(\sum_{u\in U}\|p_u\|_2^2 +\sum_{i\in I}\|q_i\|_2^2\right)$$

最近ではimplicit feedbackに対応したモデルも、もともとのexplicit feedbackのためのモデルも、共通してMFと呼ばれていることが多いので注意が必要です。

Revisiting the Performance of iALS(2022)

RecSys2022で発表された論文からは、以前のiALSとチューニング後のiALSとその他のモデルの精度比較と、性能とモデルサイズの関係性について紹介します。また、自動化されたハイパーパラメータのチューニングではなくアルゴリズムの深い知識が必要という考えのもと、この論文の最後には付録としてチューニングの指針が示されているので興味がある方は読んでみてください。

性能の再検証

これは推薦分野の研究ではよく使用される2つのデータセット (Movielens 20M, Million Song Data)での評価結果です。表中のiALSはどれもモデルとしては同じですが、ハイパーパラメータが異なることで性能が大きく変化していることがわかります。また、Deep系のモデルにも匹敵する精度が出ていることがわかります。

性能とmodel capacity

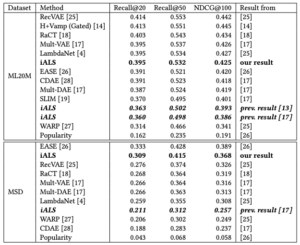
ここではmodel capacityをモデルが各アイテムに対して保有するパラメータ数と定義しています。こちらの図は以前の論文でのiALS, Multi-VAE, EASEの結果と、iALSの次元数を変化させた結果になります。次元数を上げれば上げるほど性能が向上することがわかります。iALSとMulti-VAEではmodel capacityが同じくらいの場合、精度も近しい値になっています。model capacityと性能がトレードオフと考えられます。また、ML20Mについては以前のiALSの結果と今回のiALSの結果で次元数が同じでも性能に大きな違いがあるため、他のパラメータも重要な要素になると考えられます。

EASE

EASEはWWW2019で発表された論文でitem similarityを利用する線形なモデルです。しかし、深層学習のモデルを含む様々な最新のアプローチに匹敵するランキング精度を出しており、データセットによっては最も優れた結果を出しています(特にMSD)。EASEを説明するために欠かせないのが2011年に発表されたSLIMです。EASEとSLIMはモデルの定義としては似ており、SLIMの目的関数からいくつかの要素を削ることでEASEの目的関数が出来上がるため、先にSLIMにも触れておきます。

モデル定義

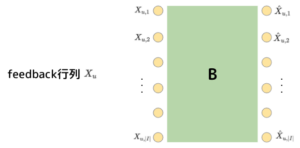
SLIMもEASEも、以下のような式と図で表すことができます。図から入力も出力もfeedback行列になっていることがわかります。この手法では、feedback行列にかけると再度feedback行列を得るような重み行列\(B\)を学習して、推薦を行います。
$$X\approx XB$$

重み行列\(B\in^{|I|\times|I|}\)はあるアイテムを好む場合にもう片方のアイテムをどれだけ好むかというアイテム同士の共起行列と捉えることができます。また、モデルを汎化させるために、\(B\)の対角行列を0とします。これは\(B\)の対角成分があるアイテムが好まれた場合にそのアイテム自身が好まれることを示す要素だからです。

ユーザ\(u\in U\)が与えられた時に、アイテム\(i\in I\)の予測スコアは以下の式で定義されます。
$$\hat{X}_{u,i} = X_{u,.}\cdot B_{.,i}$$

SLIM: Sparse Linear Methods for Top-N Recommender Systems

これはICDM2011で発表された論文で、その後も派生となるモデルが研究されてきました。この論文は当時のメモリベースの高速だが品質が劣る、モデルベースの高品質だが高速性が劣るというメリデメをどちらも解決するモデルとして登場しました。

モデルの概要は前述したので、ここではEASEへの導入のためにも目的関数について説明します。目的関数は以下のように表されます。squre lossを用いており、L1正則化とL2正則化を持ちます。一般的にL1正則化はよりデータをスパースにすることを目的に、L2正則化は過学習を防ぐために導入されます。スパース性はアイテムのsimilarityにクラスタがあることから性能や解釈性が上がったり、行列のサイズがコンパクトになることでメモリに優しく推論が速くなったりといいことが多いです。また、\(B \ge 0\)と\(\mathrm{diag}(B) = 0\)の制約があります。\(B\ge 0\)の非負制約は解釈のためによく用いられる制約ですが一般的に非負制約をはずした方が性能が高いことが知られています。後述するEASEではこの制約がなく、その点に関する比較の実験も行なっています。\(\mathrm{diag}(B) = 0\)はこのモデルを汎化させるために導入されています。

$$\underset{B}{\min}~~\|X-XB\|^2_F +\frac{\lambda_2}{2}\cdot \|B\|^2_F+\lambda_1\cdot \|B\|_1$$

$$\mathrm{s.t.}~~ B\ge 0 ,~~\mathrm{diag}(B) = 0$$

 

SLIMからEASEへ

EASEはWWW2019で発表された論文です。モデルの概要は前述したSLIMと同じですが、

• SLIMの目的関数からL1正則化と非負制約を除いたこと
• 上記に伴って、重みのが学習するための制約付き凸最適化問題が閉形式で解けるようになること

が特徴的です。EASEの重要なポイントをピックアップして説明します。

目的関数

重み行列\(B\)の学習には以下の凸な目的関数を使います。反対に前述したMF(iALSなど)の手法は非凸であるため最適化の際にALSのようにiterationが必要になります。SLIMの目的関数からL1正則化と非負制約を消した式だとわかります。
$$\underset{B}{\min}~~\|X-XB\|^2_F +\lambda\cdot \|B\|^2_F$$$$\mathrm{s.t.}~~ \mathrm{diag}(B) = 0$$

Loss: \(\|X-XB\|^2_F\)
データ\(X\)とスコア\(\hat{X}=XB\)のsquare lossを用いる理由は閉形式解の形にするためです。ranking lossを直接最適化した方がランキング精度が向上する可能性もありますが、計算コストが増大する可能性もあることに注意が必要です。

正則化: \(\lambda\cdot \|B\|^2_F\)
過学習を防ぐために学習する重み\(B\)にL2正則化を用います。そのため1つのハイパーパラメータ\(\lambda\)を持ちます。

制約: \(\mathrm{diag}(B)=0\)
この制約は、\(B=I\) (\(I\)は単位行列)になってしまわないようにするために必要になります。もし\(B=I\) となると、あるユーザに対して、以前クリックしたアイテムを再度推薦することしかできないモデルになってしまいます。( アイテム集合と単位行列が同じ表記\(I\)になってしまってすみません )

閉形式解

この\(B\)の重みを学習するための制約付き凸最適化問題は閉形式で解けることを説明します。

まずは、等式制約を目的関数に組み込み、ラグランジュ関数を形成します。
$$L=\|X-XB\|^2_F +\lambda\cdot \|B\|^2_F~~+~~2\cdot \gamma^\top \cdot \mathrm{diag}(B)$$

\(\gamma=(\gamma_{1}, ….,\gamma_{|I|})\)はラグランジュ乗数ベクトルです。この第3項は条件を満たさない、すなわち\(\mathrm{diag}(B)\neq 0\)のときに大きくなり、条件を満たす、すなわち\(\mathrm{diag}(B)= 0\)のときに0になります。制約付き最適化問題はこのラグランジュ関数を最小化することによって解くことができるのでこのラグランジュ関数の微分して、

$$\begin{eqnarray}\\
\frac{\partial}{\partial B}L &=& \frac{\partial}{\partial B}\left(\|X-XB\|^2_F +\lambda\cdot \|B\|^2_F+2\cdot \gamma^\top \cdot \mathrm{diag}(B)\right)\\
&=& -2X^\top\left(X-XB\right)+2\lambda B +2 \mathrm{diagMat}(\lambda)
\end{eqnarray}$$

上の勾配を0として、\(B\)について整理すると

$$B=\left(X^\top X+\lambda I\right)^{-1}\cdot\left(X^\top X-\mathrm{diagMat}(\lambda)\right)$$が得られます。

 

• \(\mathrm{diagMat}(\lambda)\): \(\lambda\)を対角成分にもつ対角行列
• \(I\): 単位行列

ここで、\(H=（X^\top X+\lambda I）\)とおく。
$$H=\frac{\partial^2}{\partial^2 B}L=（X^\top X+\lambda I）$$

$$\begin{eqnarray}\\
\hat{B}&=&\left(X^\top X+\lambda I\right)^{-1}\cdot\left(X^\top X-\mathrm{diagMat}(\gamma)\right)\\
&=&H^{-1}\cdot\left(H-\lambda I-\mathrm{diagMat}(\gamma)\right)\\
&=&I-H^{-1}\left(\lambda I +\mathrm{diagMat}(\gamma)\right)
\end{eqnarray}$$

\(\gamma\)は制約条件\(\mathrm{diag}(\hat{B})=0\)によって決定されるので、

$$\mathrm{diag}(\hat{B})=\vec{0}\\
\Leftrightarrow \mathrm{diag}\left(I-H^{-1}\left(\lambda I +\mathrm{diagMat}(\gamma)\right)\right)=\vec{0}\\
\Leftrightarrow \vec{1}-\mathrm{diag}(H^{-1})\odot(\lambda \vec{1} + \gamma) = \vec{0}\\
\Leftrightarrow \vec{1} = \mathrm{diag}(H^{-1})\odot(\lambda \vec{1} + \gamma) \\
\Leftrightarrow \lambda \vec{1} + \gamma = \vec{1} \oslash \mathrm{diag}(H^{-1}) \\
\Leftrightarrow \gamma = \vec{1} \oslash \mathrm{diag}(H^{-1}) – \lambda \vec{1}
$$

よりこれを\(\hat{B}\)の式に導入すると、
$$\begin{eqnarray}\\
\hat{B}&=&I-H^{-1}\left(\lambda I +\mathrm{diagMat}\left(\vec{1} \oslash \mathrm{diag}(H^{-1}) – \lambda \vec{1}\right)\right)\\
&=& I-H^{-1}\left(\lambda I +\mathrm{diagMat}\left(\vec{1} \oslash \mathrm{diag}(H^{-1})\right) – \lambda I\right)\\
&=& I-H^{-1}\left(\mathrm{diagMat}\left(\vec{1} \oslash \mathrm{diag}(H^{-1})\right)\right)
\end{eqnarray}$$

よって
$$\hat{B_{ij}} =
\begin{cases}
0 & (i=j)\\
-\dfrac{(H^{-1})_{i,j}}{(H^{-1})_{jj}} & (otherwise)
\end{cases}
$$

\(\hat{B}\)は非対称行列ですが、\(H^{-1}\)は対称行列です。\(B\)を推定するためにデータから計算しておく必要のある値 (十分統計量)はアイテム\(\times\)アイテムの行列であるグラム行列\(G=X^\top X\)によって与えられます。

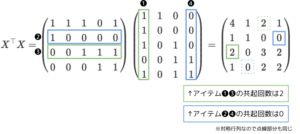
ここで、\(G=X^\top X\)とはどのような行列なのかをユーザ数5、アイテム数4の例で考えてみます。この場合のfeedback行列\(X\)は、以下のように表すことができ、ユーザ①はアイテム❶❷をクリックしているなどがわかります。ユーザ軸で行をくり抜くと、ユーザ\(u\)がどのアイテムをクリックしたかを表すベクトルと捉えることができます。反対にアイテム軸で列をくり抜くと、アイテム\(i\)がどのユーザにクリックされたかを表すベクトルと捉える事ができます。

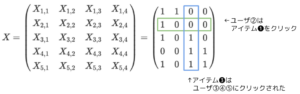
また、\(G=X^\top X\)は以下のように示すことができます。このとき\(G\)の各要素はアイテム間の共起回数を表していることがわかります。この\(G\)を利用して、あるアイテムがクリックされているときに別のアイテムをクリックするであろう確率を示す\(B\)が推定されます。

計算量

\(G=X^\top X\)の計算については大規模なデータ処理ができるシステムを使って事前計算しておくとよいです。ここで\(G\)は\(|I|\times |I|\)の行列です。

事前計算をした場合に残りの計算量は、\(G=X^\top X\)の逆行列の計算で決まります。基本的なアプローチの場合には\(\mathcal{O}(|I|^{3})\)、Coppersmith-Winograd algorithmを利用した場合には\(\mathcal{O}(|I|^{2.376})\)になります。(逆行列の計算は\(O(|I|^3)\))

また、\(G=X^\top X\)は事前に計算されるため、ユーザ数にもユーザ-アイテム間のインタラクション数にも依存しません。そのため、アイテム数が少ないデータセットに関しては特に有用であることがわかります。また、feedback sparsityより疎行列\(X\)のグラム行列\(G\)の計算は高速です。もととなるSLIMやその派生の計算コストと比べても桁違いに低いことがわかります。

SLIMとの比較

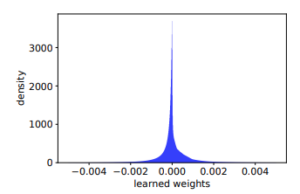
論文の5.2では、SLIMとの差分である非負制約とL1正則化について考察されています。以下に示しているのは重みの分布です。正負どちらにも値があることから、アイテム間の類似度（正の重み）だけでなく、非類似度（負の重み）をも学習することが重要であることを示しています。
また、EASE+非負制約の性能はほぼSLIMと同じことからSLIMのL1正則化はあまり効いていなかったとも考えられます。ただ、L1正則化だけ抜いた場合は再現できないため、SLIMでは閉形式解がなく、EASEよりも最適化が難しいことによるものかもしれません。

関連する非線形モデル

今まで線形モデルの話をしてきたので少し横道にそれますが、非線形モデルについても少し触れておきます。今までのモデルと非線形モデルでは全く違うかと思いきや、意外と通づる部分があるからです。近しい部分や差分についても交えて説明できたらと思います。

Auto-Encoder

近年だと協調フィルタリングにディープニューラルネットワークをベースとしたAuto-Encoderを用いたモデルが多く研究されています。ここまで線形モデルの話をしてきましたが、Auto-Encoderを用いた非線形モデルとも関連性があるので、いくつかの論文について紹介します。

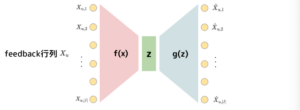
Auto-Encoderとは、あるデータの入力に対して、同じデータが出力となるように学習される、次元圧縮や次元削減に利用されるモデルです。Auto-Encoderを利用したモデルが協調フィルタリングの手法に用いられ始めたのは、WWW2015のAutoRecやWSDM2016のCDAEです。モデルを以下に図示してみると、前述したSLIMやEASEの非線形版と捉えることができます。

 

CDAE: Collaborative Denoising Auto-Encoders for Top-N Recommender Systems(2016)

implicit feedbackはユーザの嗜好データの欠損版と考えることができます。すなわちユーザの嗜好データの欠損版からユーザの完全な嗜好データを学習することで、観測してない(欠損していた)ユーザの嗜好スコアを算出できるようにしているとみなせます。

そこで、意図的にシミュレーション(dropout)によってランダムに作り出した欠損を復元するように学習する点がimplicit feedbackにおける推薦の課題に近しいと考え、Denoising Auto-Encoderを利用した推薦が2016年に提案されました。

Variational Autoencoders for Collaborative Filtering(2018)

最近ではVariational Autoencoderを用いたモデルが多く研究されています。単純なAuto-EncoderとVariatioanl Auto-Encoderの違いは\(z_u\sim \mathcal{N}(0,1)\)とする点です。こちらの手法はVAEを用いていますが、尤度関数としてVAEでよく用いられるガウス分布やベルヌーイ分布ではなく、多項分布を用いるためMult-VAEと呼ばれています。

$$z_u\sim \mathcal{N}(0,I_K),~~~\pi(z_u) \propto\exp{f_\theta(z_u)},\\
x_u \sim \mathrm{Mult}(N_u, \pi(z_u))$$

非線形関数\(f_\theta\)はパラメータ\(\theta\)の多層パーセプトロンであり、出力はsoftmaxによって正規化され、アイテム集合全体に対する確率ベクトル\(\pi(z_u)\in \mathbb S^{I-1}\)が生成されます。ユーザ\(u\)からクリック数\(N_u = \sum_i x_{u,i}\)が与えられたとき、\(x_u\)は確率\(\pi(z_u)\)の多項分布からサンプリングされると仮定します。この生成モデルは潜在因子モデルを一般化していて、\(f_\theta\)を線形とし、ガウス尤度を用いることで古典的なMFの形になります。

これはユーザがどのアイテムを1番好むかというアイテムそれぞれのtop-1 probabilityのモデルとして\(\pi (z_u)\)があると捉えることができます 。したがってモデルはあるアイテムが独立にどれくらいクリックされるかという二値問題ではなく、アイテムの中でどれが1番になるかという問題を解くことになり、推薦システムが一般に評価されるtop-Nランキング問題にうまく機能するようになると考えられます。また、このMult-VAEでも先行研究(CDAE)と同様にDenoisingが行われています。

 

Enhancing VAEs for Collaborative Filtering: Flexible Priors & Gating Mechanisms (2019)

この論文はH+Vamp(Gated)と略されることが多く、貢献ポイントはその名の通り、階層化とVampPriorとGating機構の導入です。それまでのVAEを用いた推薦モデルではVAEで用いる事前分布がユーザーの嗜好を学習するためには単純すぎると考え、より柔軟な事前分布を設定するために画像処理などで用いられるVampPrior (variational mixture of postiors prior)を利用しています。変分後の混合分布を用いて事前分布を近似します。さらにVampPriorsの原著のようによりリッチな潜在的表現を学習するために、Hierarchical Stochastic Unitsを採用しています。
$$p_{\lambda}(z)= \frac{1}{K}\sum_{K=1}^K q_\phi(z|u_k) \ $$

また、Auto-Encoderを推薦システムに活用する先行研究では比較的浅いネットワークを利用しており、隠れ層を増やしてもあまり性能が向上しないことが知られています。これは①スパースなfeedback行列からユーザの嗜好を抽出するというデータの性質や②encoderとdecoderという比較的簡単に深くなりやすい構造上だと考えられます。そこで、ネットワークのmodeling capacityを高めるために、より深いネットワークでの情報伝搬を助けるために提案されたGated CNNで提案されたゲーティングの機構を導入しています。

RecVAE: A New Variational Autoencoder for Top-N Recommendations with Implicit Feedback(2020)

こちらもVAEを用いた推薦モデルで、Mult-VAEの改良として報告されています。貢献としては、事前分布にComposite priorを利用、アーキテクチャの変更、ハイパーパラメータβの設定方法、交互更新を行う新しい学習方法の提案などがあります。アーキテクチャでは、dense CNNsから着想を得たdensely connected layersやswish activation functions、層の正則化を導入したことが特徴的です。decoderはsoftmaxの単純な線形層で、\(\theta = \{W, b\}\)です。ここで、\(W\)と\(b\)はそれぞれアイテムのembedding行列とアイテムのbiasベクトルと捉えることができます。また、同様にencoderはユーザからのfeedbackをユーザembeddingにマッピングする関数と考えることができます。

次に、事前分布にComposite priorを使っていることについてです。標準正規分布と、前のエポックから引き継がれた固定パラメータによる近似事後分布の組み合わせとする複合事前分布を用いています。第2項はパラメータ最適化の際の大きなステップを抑制するauxiliary loss functionとして解釈でき、第1項はoverfittingを防止します。
$$p(z|\phi_{old}, x) = \alpha \mathcal{N}(z|0 , I)+(1-\alpha)q_{{\phi}_{old}}(z|x)$$

最後に交互更新による学習についてです。これはALSで行われているようにユーザとアイテムを交互に最適化していくものです。アーキテクチャの話で前述したようにencoderをユーザembeddingのマッピングの関数、decoderの\(\theta = \{W, b\}\)はそれぞれアイテムのembedding行列、アイテムのbiasベクトルと捉えることができ、encoderとdecoderのそれぞれのパラメータは異なる性質を持っていると捉えることができるので、異なる方法で学習します。また、denoisingが重要であることはこの実験でも先行研究(CDAE)でも確認できていることなのですが、この研究ではdecoderのdenoisingだけを無くしてみると結果が良くなったようです。他の正則化手法でも結果が性能が下がったことからoverregularizedであると考えられます。

Sequential Recommendation

DAEではシミュレーションによって生み出した欠損を埋めることで学習をしていますが、実際のデータの観測過程を考慮して、過去から未来を予測してもいいのではないかと考えることができます。また、今までの手法だと順番を考慮はできていませんでした。そこで、よく研究されているのがSequential Recommendationです。RecSys2022のベストペーパーもSequential Recommendationで、最近のホットなトピックです。ただ少し問題設定が違うことに注意は必要ですが、考え方として近しいと思います。Sequential Recommendationと、これまで見てきたモデルの大きな違いはfeedback行列、すなわちfeedbackのサブセットを入力とするか、時間情報を持つfeedbackを入力とするかです。VAEの派生としてもsequentialなencoderを用いた研究もあります。また、他にもたくさんのsequentialはモデルが研究されていますが、transformerベースの手法だと、順番だけじゃなく時間間隔も反映する研究が行われています。

 

実務活用

ここまではそれぞれのモデルについて説明してきましたが、実際にエンジニアが推薦システムをサービングしようとする場合のことについても少し説明します。

システム構成

最も簡単な構成から説明します。学習も推論も定期実行などのバッチ処理で行った結果をDBに格納しておいて、リクエスト時にはDBに格納された推論結果を返すだけという方法です。推薦システムの導入初期やすごく重いモデルを利用したい場合に使われる構成です。この構成の欠点は、リアルタイム性が低くなることです。そのため、1日1回のpush通知の推薦など、リアルタイム性に重要度がないシステムの場合にも有効かもしれません。

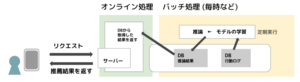
次に多くのサービスで採用されているであろうシステム構成について説明します。モデルの学習を毎時または数時間に1回、1日に1回などのバッチ処理で行い、推論はオンライン処理で行う構成です。システムの構成を簡単に図示しました。リアルタイム性が重要な場合にはこの構成になると思います。推論部分だけをオンライン処理することによって、学習からリクエストまでの間に溜まったデータを利用するからです。しかし、ユーザのリクエストが来てから推論を実行するため推論のレイテンシがシビアになってきます。また、バッチ処理の学習でも時間が長くかかってしまう場合にはいつまで古いモデルを使い続けてしまうことになるので、毎時更新なら1時間など短い時間で学習が完了することも重要になってきます。

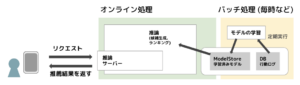
学習時間と推論レイテンシ
上記よりシステムの構成によって求められる推論のレイテンシと学習時間が変わります。Deep系のモデルではiterationの回数が多く学習時間が長くなるため、頻度の高いモデル更新を行う場合には向かないかもしれません。そのためMFのように予測が内積計算だけのようなモデルでは推論時は内積計算だけで済むので、比較的推論のレイテンシを抑えられることも魅力です。これはMFのような線形モデルに限らず、Deep系のモデルでもユーザとアイテムのembeddingを出力して内積を取るようなモデルに対して共通です。ただ、MFのようにユーザとアイテムのembeddingを全て保存しておく必要のあるモデルでは、単純にモデルを保存しておくだけのモデルに比べて、ストレージのコストがかかることが懸念点として挙げられます。

コールドスタート

MFでは推論時に学習済みのユーザ因子ベクトルとアイテム因子ベクトルが必要なことから、学習時にデータのないユーザまたはアイテムは推薦の対象にできないという問題があります。そこで学習から推論までの間に獲得した行動履歴のデータを用いて、推論時にユーザベクトルを擬似的に作成することで推薦可能にする手法もあります。

また、EASEやAuto-Encoder系の手法では、学習済みのユーザベクトルなどは必要なく、ユーザの行動履歴さえあれば予測可能であるため、新規のユーザにもそのまま対応できます。

どちらの場合でもユーザの行動履歴の差分は扱いやすいですが、新規のアイテムについてはさらに工夫が必要であることに注意が必要です。

おわりに

協調フィルタリング、特に線形モデルに焦点を当ててまとめてみました。実際に自分の言葉で書いてみることで、今までわかっているつもりになっているだけだったことに気づいたり、より深い理解が得られたり、とても勉強になりました。また、複数のモデルを一気にサーベイすることで、似ている点などが見えてきたのも面白かったです。

このブログでは線形モデルを中心にまとめていましたが、ここ数年はSequential Recommendationが多く研究されており、transformerなどは元自然言語処理の人としては馴染みの深いモデルが使われている分野なので、そのあたりももう少し深掘って行きたいなと思いました。またコールドスタートや分散処理のシステム構成をはじめとする実際の仕事でどう使っているかの話でもブログが書けるといいなと思いました。

今後も推薦アルゴリズムの勉強を継続しつつ、分散処理やユーザ理解などの力を蓄えて、ユーザの素敵な出会いをちょっとサポートできるように頑張ります。

出典

• [1] Y. Hu, Y. Koren and C. Volinsky, “Collaborative Filtering for Implicit Feedback Datasets,” 2008 Eighth IEEE International Conference on Data Mining, 2008, pp. 263-272, doi: 10.1109/ICDM.2008.22. https://ieeexplore.ieee.org/document/4781121
• [2] Steffen Rendle, Walid Krichene, Li Zhang, and Yehuda Koren. 2022. Revisiting the Performance of iALS on Item Recommendation Benchmarks. In Proceedings of the 16th ACM Conference on Recommender Systems (RecSys ’22). Association for Computing Machinery, New York, NY, USA, 427–435. https://doi.org/10.1145/3523227.3548486
• [3] Harald Steck. 2019. Embarrassingly Shallow Autoencoders for Sparse Data. In The World Wide Web Conference (WWW ’19). Association for Computing Machinery, New York, NY, USA, 3251–3257. https://doi.org/10.1145/3308558.3313710
• [4] X. Ning and G. Karypis, “SLIM: Sparse Linear Methods for Top-N Recommender Systems,” 2011 IEEE 11th International Conference on Data Mining, 2011, pp. 497-506, doi: 10.1109/ICDM.2011.134. https://ieeexplore.ieee.org/document/6137254
• [5] Suvash Sedhain, Aditya Krishna Menon, Scott Sanner, and Lexing Xie. 2015. AutoRec: Autoencoders Meet Collaborative Filtering. In Proceedings of the 24th International Conference on World Wide Web (WWW ’15 Companion). Association for Computing Machinery, New York, NY, USA, 111–112. https://doi.org/10.1145/2740908.2742726
• [6] Yao Wu, Christopher DuBois, Alice X. Zheng, and Martin Ester. 2016. Collaborative Denoising Auto-Encoders for Top-N Recommender Systems. In Proceedings of the Ninth ACM International Conference on Web Search and Data Mining (WSDM ’16). Association for Computing Machinery, New York, NY, USA, 153–162. https://doi.org/10.1145/2835776.2835837
• [7] Dawen Liang, Rahul G. Krishnan, Matthew D. Hoffman, and Tony Jebara. 2018. Variational Autoencoders for Collaborative Filtering. In Proceedings of the 2018 World Wide Web Conference (WWW ’18). International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, CHE, 689–698. https://doi.org/10.1145/3178876.3186150
• [8] Ilya Shenbin, Anton Alekseev, Elena Tutubalina, Valentin Malykh, and Sergey I. Nikolenko. 2020. RecVAE: A New Variational Autoencoder for Top-N Recommendations with Implicit Feedback. In Proceedings of the 13th International Conference on Web Search and Data Mining (WSDM ’20). Association for Computing Machinery, New York, NY, USA, 528–536. https://doi.org/10.1145/3336191.3371831
• [9] Noveen Sachdeva, Giuseppe Manco, Ettore Ritacco, and Vikram Pudi. 2019. Sequential Variational Autoencoders for Collaborative Filtering. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining (WSDM ’19). Association for Computing Machinery, New York, NY, USA, 600–608. https://doi.org/10.1145/3289600.3291007
• [10] Jiacheng Li, Yujie Wang, and Julian McAuley. 2020. Time Interval Aware Self-Attention for Sequential Recommendation. In Proceedings of the 13th International Conference on Web Search and Data Mining (WSDM ’20). Association for Computing Machinery, New York, NY, USA, 322–330. https://doi.org/10.1145/3336191.3371786