本記事は、CyberAgent Advent Calendar 2022 14日目の記事です。

目次

1. はじめに
2. 相互推薦システム
3. 関連研究
   • Su et al. (2022)
   • Chen et al. (2021)
4. マッチング理論に基づく相互推薦システム
5. まとめ

はじめに

こんにちは！AI Lab経済学社会実装チームでリサーチサイエンティストとして働いているみーとみ（@miiitomi）です。

みなさん、突然ですが、恋してますか？僕は今年も恋人ができず、12月24日は例年通り世のカップルどもを呪って過ごすことになりそうです。という僕の私怨は置いといて、近年結婚・恋愛市場は変化しつつあるようです。明治安田生命が2022年11月に発表した「いい夫婦の日」に関するアンケート調査によると、2015年〜2019年に結婚した人で夫婦の出会いのきっかけは「マッチングアプリ」だったと回答した人は6.6%であったものの、2020年以降に結婚した人では18.8%、2022年単年では22.6%と5人に1人以上に上り、マッチングアプリで出会った人と結婚する人の割合は増加しています。

マッチングアプリのようなプラットフォームにおいて、どのユーザーをどの順番で表示するかを決定する推薦システムは、ユーザー体験に大きな影響を与えます。推薦システムはECサイトや動画配信サービスなど多くのWEBサービスにおいて活用されていますが、マッチングアプリのようにユーザーに他のユーザーを推薦するという形になっているものは特に相互推薦システムと呼ばれており、マッチングアプリの他に求人・求職サービスの分野でも研究・開発がされています。

ECサイトや動画配信サービスなどの通常の推薦システムでは推薦されるものは商品や動画ですが、相互推薦システムではユーザーにユーザーが推薦されます。多くの人から好まれる人気なユーザーを過剰に推薦することは、ユーザーの被推薦機会に偏りが生じ不公平であるというだけでなく、人気ユーザーに過剰にいいねが集まってもその一ユーザーが実際にやり取りが可能な人数は限られることから「多くのユーザーに多くの出会いを提供する」というマッチングプラットフォーム目的と照らし合わせても望ましくありません（もちろん通常の推薦システムにおいても人気商品ばかりを過剰に推薦することは望ましくないでしょうが、被推薦機会の偏りが問題となる状況はマッチングサービスなど相互推薦システムの方が多いでしょう）。したがって相互推薦システムにおいては、ユーザー間の相互の興味と、各ユーザーがマッチ可能な人数（キャパシティ）を考慮した上で、被推薦機会が過度に人気ユーザーに集中しすぎないように設計することが重要であると考えられます。

本記事では相互推薦システムの概要と、上述の課題感に沿った関連研究を紹介した上で、現在進行中の私たちの研究・実装プロジェクトについて説明していきたいと思います。

相互推薦システム

相互推薦システムでは、アイテム（商品や動画など）をユーザーに推薦する通常の推薦システムと異なり、ユーザーにユーザー（求人サービスでは求職者と企業、マッチングアプリでは男性と女性）を推薦します（本節では求職者・企業を例に説明します）。ある求職者Aが企業Bに対し興味を持つだろうと予測されても、企業Bが求職者Aに興味を持たないだろうと予測される場合、求職者Aに企業Bを推薦することは有効的でありません。したがって、ユーザー間の相互の興味の一致度を考慮して推薦することが重要となります。

通常の相互推薦システムではまずサービス上の行動履歴や属性データから、各求職者 \(x\) が各企業 \(y\) に対しどれだけ興味を持つかを予測する興味スコア \(p_{x,y}\) と、逆の各企業 \(y\) から各求職者 \(x\) への興味スコア \(p_{y,x}\) を、それぞれ行列分解（Matrix Factorization）などの推薦・機械学習手法により計算します。そしてユーザー間の相互の興味の一致度を考慮するため、\(p_{x,y}\) と \(p_{y,x}\) をなんらかの集約関数 \(\phi(p_{x,y}, p_{y,x})\) にかませて相互興味スコア \( p_{x \leftrightarrow y}\) を計算し、そのスコア順に推薦を行うというやり方が一般的です。集約関数には主に算術平均や幾何平均などが使われていることが多いようです。

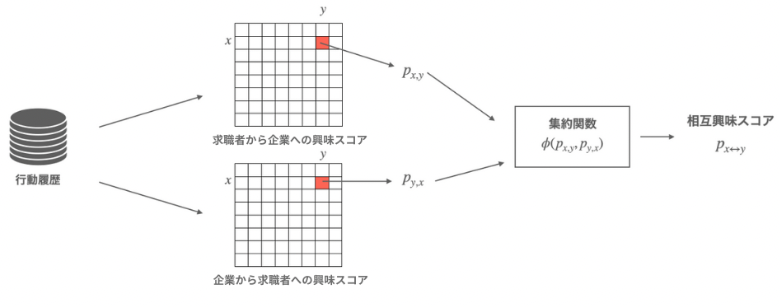
このように単純な集約関数を用いた手法では、ユーザー間の相互の興味の一致度は考慮することはできても、ユーザーのマッチ数上限・キャパシティは考慮できていないと思われます。例えば、どの求職者からも興味をもたれるような人気企業 \(y\) があった場合、それはどの求職者 \(x\) に対しても片側の興味スコア \( p_{x,y} \) は高くなるため、相互の興味スコア \(p_{x \leftrightarrow y}\) も高くなる傾向になり、この人気企業 \(y\) が過度に被推薦機会を集めるといったことが起こり得るでしょう。被推薦機会を偏りすぎないようにして不平等を緩和し、全体のマッチ数やユーザー満足度を高めるようにするためには、計算された片側の興味スコアから推薦に利用するスコアへの計算過程を、より精緻なものにする必要があります。

関連研究

前節で述べたような課題感に対して取り組んでいる関連研究を2つ紹介します。

Su et al. (2022)

Su et al. (2022)では、求人を行っている企業と求職者のマッチングプラットフォームにおいて、求職者は提示された企業のランク付きリストから興味のある企業に応募し、企業は応募を受けた求職者のランク付きリストからマッチする求職者を選ぶ、という状況を考えます。各求職者・企業がどの企業・求職者に対しどれだけの確率で興味を持つかは事前に予測ができているものとし、ここでプラットフォームが決めたいものは各求職者に提示する企業のランク付きリストです。

各求職者・企業は興味確率と提示されたランク付きリストに対し、Position-Based Model (PBM)に従って応募・マッチすると仮定します。PBMではリストの下位に行くほど応募・マッチする確率が減少していきます。人気企業を多くの求職者に提示して多くの応募を人気企業に集めても、その企業に提示されるリストにおいて多くの応募はリストの下位に位置付けられてしまうことになりマッチ数は多くならないため、求職者に対して単純に興味の高い企業を上から推薦していく方法は効果的でありません。したがって、このPBMの仮定が上述のキャパシティのような役割を果たします。

Su et al. (2022)は、各求職者に提示する企業のランク付きリストを決めた時の、プラットフォーム全体の期待マッチ総数を社会厚生関数と定義し、この社会厚生関数を最大化するランク付きリストを見つけることを目的とします。そして、社会厚生関数の下限となり最大化の目的関数として扱うことのできるような関数を求め、その最大化を行うことを提案しています。

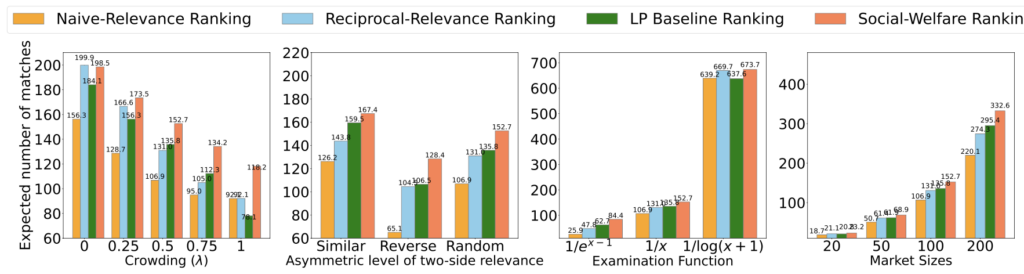
人工データおよび学会におけるネットワーキングシステムのデータを用いた実験において、単純に求職者の企業への興味順に推薦するナイーブな手法や、求職者から企業への興味と企業から求職者への興味を掛け合わせたものをスコアとして推薦するReciprocal-Relevanceといった手法と比較し、社会厚生関数を用いた提案手法がより多くのマッチ数を生むことを示しました。特に、一部の人気企業に求職者からの人気が集中しているようなケース（上図一番左でCrowdingパラメータのλが大きいケース）では、より提案手法が効果的となっています。

Chen et al. (2021)

Chen et al. (2021) では、台湾のオンラインデーティングサービスにおいて、ユーザーへ異性のユーザーを推薦する相互推薦システムを考えます。ユーザーを属性（収入や学歴など）に基づきグルーピングした上で、ユーザーの異性ユーザーへの興味スコアはユーザー属性と特徴量とするOLS (Ordinary Least Squares)により計算します。そしてTUマッチング（Matching with Transferable Utility）の分野におけるChoo and Siow (2006)のモデルに基づき安定マッチングを計算し、そのスコアによって推薦を行います。

TUマッチングモデルは主に経済学において労働市場や結婚市場の分析に用いられ発展してきた分野です。労働者と企業、あるいは男性と女性がマッチ（雇用契約、結婚）した場合、両者間で効用移転（賃金、所得移転など）が行われるとし、その移転額が市場における価格のように働いて需要と供給が調整されます。よって均衡においては両者の需要が一致するようにマッチが形成されると想定されます。このTUマッチングモデルに基づいてオンラインデーティングにおける推薦を行うことで、人気ユーザーに推薦機会を集め過ぎることなく適切な推薦が行われると考えられます。

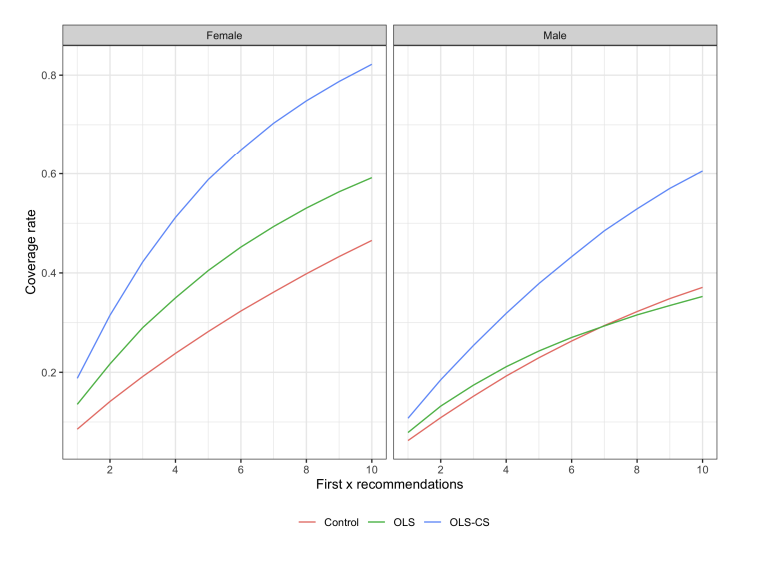
Chen et al. (2021) では台湾のオンラインデーティングサービスにおいて実際にオンライン実験を実施しました。Control（詳細は伏せられています）とOLS（単純にユーザーに興味スコアの高いユーザーを推薦する手法）と比較し、被推薦機会はより平等になっています（上図Covorage rate）。また、総マッチ数は減少しているものの、マッチ数のユーザー中央値や平等性に関する指標（分散やジニ係数）は改善しています。

マッチング理論に基づく相互推薦システム

前節で紹介した2つの関連研究は私たちの課題感に沿うものではあるものの、そのままでは実際にマッチングプラットフォームにおいては実装が困難です。Su et al. (2022) はPosition-Based Modelの仮定と想定されているプラットフォームの設定に依存するとともに、数万〜数十万規模のマッチングプラットフォームにおいては計算が不可能であるような計算量の手法となっています。一方、Chen et al. (2021) ではユーザーを属性でグルーピング際に粒度が粗くなってしまい、行動履歴データを用い細かくパーソナライズされた推薦を行うことができません（オフライン実験では行列分解を用いて計算した興味スコアに対しChoo-Siowモデルの安定マッチングを計算する実験も行っていますが、こちらもおそらく計算量の問題でサンプリングされた一部のユーザーに対してのみ行っています）。

私たちはTomita et al. (2022) において、マッチング理論に基づく相互推薦システムを提案しました。ユーザーの行動履歴から行列分解などの推薦の手法により求職者から企業、企業から求職者への片側の興味スコアを計算するのは従来の相互推薦システムと同様です。それらを組み合わせる際、2グループ間の相互の興味（選好）とマッチ上限（キャパシティ）をもとに適切なマッチを考える「マッチング理論」の分野のアルゴリズムによってスコアを計算し、推薦を行います。実際に計算するマッチングアルゴリズムはいくつか考えられますが、現状私たちのプロジェクトではChen et al. (2021) と同様TUマッチングの分野のChoo-Siowモデルによって計算しています。

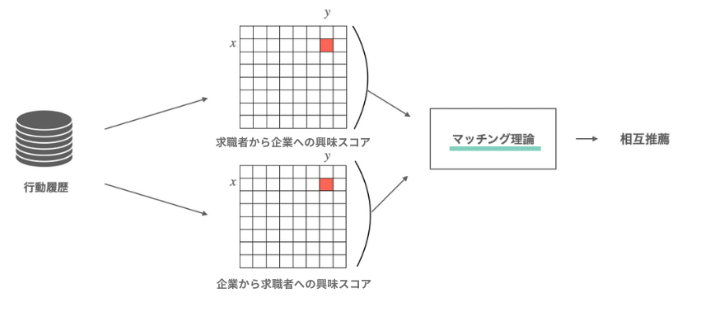
ただし、数万〜数十万ユーザー規模のプラットフォームでは安定マッチングの計算は困難です。そこで私たちは安定マッチングの計算更新式の一部で近似計算を行うことにより、実行可能なマッチング理論に基づく相互推薦システムを実現しました （詳しくは元論文をご覧ください）。

ここで紹介したマッチング理論に基づく相互推薦システムは、マッチングアプリ「タップル」での導入を目指し、現在研究・開発を行っています。

まとめ

マッチングアプリなどのプラットフォームにおける相互推薦システムでは、ユーザー間の相互の興味の一致度だけでなく、ユーザーが実際にマッチ可能な（やり取り可能な）人数上限（キャパシティ）を考慮した上で推薦を行うことが、被推薦機会の過度な集中を避け不平等を緩和する観点からもユーザー全体のマッチ数・満足度の改善する観点からも重要です。2グループ間の相互の興味・選好と、人々のマッチング上限・キャパシティをもとに適切なマッチを考える「マッチング理論」という分野が経済学やコンピュータサイエンスにおいて研究されており、マッチングプラットフォームにおいてもこのマッチング理論に基づく相互推薦システムが有用であると考えられます。

本記事では相互推薦システムの概要と、私たちの取り組んでいるマッチング理論に基づく相互推薦システムを関連研究と併せて紹介しました。これからも皆が幸せになるマッチングプラットフォームを目指して、相互推薦システムの研究・開発に取り組んでいきたいと思います。僕も1年後の12月24日は周りを恨まず明るい気持ちで過ごせるよう、来年は恋活を頑張りたいです。上手くいったかどうかの答え合わせは来年の CyberAgent Advent Calendar 2023 で！！

引用文献

• Chen, Kuan-Ming, Yu-Wei Hsieh and Ming‐Jen Lin. 2021. “Reducing Recommendation Inequality via Two-Sided Matching: A Field Experiment of Online Dating.” Available at SSRN: https://ssrn.com/abstract=3718920.
• Choo, Eugene and Aloysius Siow. 2006. “Who marries whom and why.” Journal of Political Economy 114.1 (2006): 175-201. https://doi.org/10.1086/498585.
• Su, Yi, Magd Bayoumi and Thorsten Joachims. 2022. “Optimizing Rankings for Recommendation in Matching Markets.” In Proceedings of the ACM Web Conference 2022 (WWW ’22). https://doi.org/10.1145/3485447.3511961.
• Tomita, Yoji, Riku Togashi and Daisuke Moriwaki. 2022. “Matching Theory-based Recommender Systems in Online Dating.” In Proceedings of the 16th ACM Conference on Recommender Systems (RecSys ’22). https://doi.org/10.1145/3523227.3547406.