はじめに
2023年9月の1ヶ月間、AI事業本部協業リテールメディアディビジョンにて、「CA Tech JOB」というインターンシップに参加した東京大学大学院経済学研究科修士1年の西田鴻志です。
本記事では、インターンシップ中に取り組んだ、短期で観測できる指標を活用した長期的な処置効果の推定と、その小売データ分析への応用について紹介します。
背景
施策の効果検証において、その長期的な影響について関心があることは多いと思います。例えば、あるマーケティング施策について、施策直後の売上といった短期の影響だけでなく、顧客生涯価値（LTV）といった長期的な影響を知りたいというニーズがあります。協業リテールメディアディビジョンにおいても、施策の長期的な効果を評価するための分析は行われていました。
長期的な効果を分析するときには、分析に必要なデータを観測するために時間がかかるという課題があります。これにより、データを待つ間にPDCAサイクルが停滞してしまうことも考えられます。しかし一方で、それを避けるために、施策開始から短期間のうちに分析しようとした場合、この時点では施策の影響が反映された長期指標のデータはありません。
そこで今回のインターンでは、施策開始後の短期間に得られるデータを用いて、長期指標への効果をより迅速に、より正しく推定するためのアプローチを検討しました。
論文調査
上述の背景から、長期指標に関連する手法の論文サーベイから始めました。
長期指標の分析について、
- 生存時間分析：施策があるイベントの発生までの時間に与える影響を分析
- 動学モデルの構造推定：消費者の継時的な購買行動を効用最大化行動として分析
などの手法があります。これらは計量経済学の分野で伝統的に用いられており、マーケティングでも多くの応用例があります。経済学がバックグラウンドの自分は、以前から馴染みがあったこれらの手法を用いることを当初は考えていました。しかし、今回のインターンの小売データの分析においては、これらの手法が必ずしも最適とは限らないという課題がありました。
生存時間分析については、サブスクリプションサービスなどでよく用いられますが、小売業のような領域では応用例が少なく、分析すべき継続時間を設定するのが困難だと考えました。一方で、動学モデルの構造推定は小売業での応用例があるものの、この手法を用いた分析には時間がかかるため、1ヶ月のインターンシップ期間では検証が難しいと考えました。また、これらの手法を用いて顧客生涯価値をはじめとした長期指標を分析する際には、モデルの特定化の問題があったり、モデルに強い仮定を置く必要があったりします。
そこで、論文サーベイを経て、以下で詳述する Athey et al. (2019) の Surrogate index による方法を用いることにしました。この手法は、比較的短期間で手に入る中間指標を上手く活用することで、施策から長期指標への効果を短期間のうちに測定することができます。
Surrogate index を用いた長期的な処置効果の推定
設定
本記事では、一般的で厳密な議論は元論文に譲るとして、Surrogate index による長期的な処置効果の推定方法を直感的に説明します。説明を単純にするため、処置がランダムに割り当てられている実験的な状況を考えます[1]。
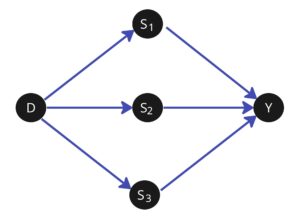
この実験サンプルデータにおいて、ルービンの因果モデルに基づいて記法を導入します。個人を表す変数を \(i\) とし、処置を受けたときに1、受けなかったときに0をとる2値の処置変数を \(D_i\) とします。各個人について、処置を受けたとき・受けなかったときの Surrogate variable（中間変数[2]）の潜在結果変数のベクトルを \(\{S_i(1), S_i(0)\}\) 、長期指標の潜在結果変数を \(\{Y_i(1), Y_i(0)\}\) で表します。また、この手法では \(D_i\) から \(Y_i\) への直接効果がない状況を考えます。
これらの変数を用いて、実験サンプルデータにおいて実際に観測される \((S_i, Y_i)\) は
\[S_i = D_iS_i(1) + (1-D_i)S_i(0)\]
\[Y_i = D_iY_i(1) + (1-D_i)Y_i(0)\]
と表せます。マーケティングの文脈では、\(D_i\) としてはマーケティング施策、\(Y_i\) としてLTV、\(S_i\) として短期間の売上や来店頻度などを考えることができます。ここで、Surrogate index \(h(s)\) は
\[h(s) := E[Y_i|S_i = s]\]
となり、中間変数で条件付けた \(Y_i\) の期待値と定義されます。このSurrogate indexを用いることで、短期的な売上・来店頻度といった中間指標 \(S_i\) のデータが存在している個人のLTVの予測値を、各個人 \(i\) ごとに得ることができます。このように、Surrogate indexは実験サンプルにおいて未観測の長期指標 \(Y_i\) を代用するために用います。
手元にある利用できるデータには、施策実施時から短期のデータ \((D_i, S_i)\) を含む実験サンプルデータに加えて、短期から長期のデータ \((S_i, Y_i)\) を含む過去サンプルデータの二つがあるとします。このように、Surrogate indexによる推定方法は、短期しかわからない実験データと、長期間の過去データがある状況で、施策の長期的な効果を測るために用いることができます。例えば、本稿後半で述べるデータ分析では、数年分の行動ログがある過去データを活用して、つい最近行った施策の長期効果を測るという応用を行いました。以下で述べる通り、この過去サンプルデータは、実験サンプルにおいて未観測の \(Y_i\) を代用する \(h(s)\) を推定するために用います。
推定方法
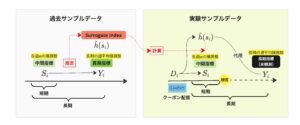
もし、実験サンプルデータにおいて長期指標 \(Y_i\) が観測されるならば、処置群での平均 \(\bar{Y_1}\) と対照群での平均 \(\bar{Y_0}\) を用いて、長期的な処置効果 \(\tau = E[Y_i(1) – Y_i(0)]\) は \(\bar{Y_1} – \bar{Y_0}\) で推定できます。しかし、今回は施策から短期間のうちに長期的な効果を測ろうとしています。その場合、短期には実験サンプルデータにおいて長期指標 \(Y_i\) が観測されず、実際にはこの推定はできません。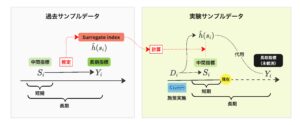
そこで、Surrogate index を用いたアプローチでは、次の方法で長期的な処置効果を推定します。
まず、過去サンプルデータを用いて、中間変数を条件づけたときの長期指標の期待値 \(h(s)\) を推定します。ここで、推定された \(h(s)\) を \(\hat{h}(s)\) とします。次に、その推定結果を用いて実験サンプルデータで \(\hat{h}(s_i)\) を計算します。そして、処置群での \(\hat{h}(s_i)\) の平均 \(\bar{h}_1\) と対照群での \(\hat{h}(s_i)\) の平均 \(\bar{h}_0\) を用いて、長期的な処置効果の推定量を \(\hat{\tau} = \bar{h}_1 – \bar{h}_0\) とします。この推定量は、
- \(D_i\) から \(Y_i\) への直接効果がない：処置 \(D_i\) から長期指標 \(Y_i\) への効果は全て中間変数 \(S_i\) を経由する。
- 中間変数 \(S_i\) と長期指標 \(Y_i\) の間の関係が、過去サンプルデータと実験サンプルデータで変わらない：そのため、過去サンプルデータで推定した Surrogate indexを、実験サンプルデータにおける未観測の \(Y_i\) を代用するために用いることができる。
という仮定の下で、長期的な処置効果 \(\tau\) を正しく推定することができます。
ここでのポイントは、短期では観測できない \(Y_i\) を、短期で観測できる中間変数から計算される \(\hat{h}(s_i)\) で代用することで、施策から短期間のうちに長期的な処置効果が推定できるという点です。
小売データを使った分析
Surrogate index を用いた長期的な処置効果の推定がどの程度うまく機能するかを、実際のデータを用いて検証しました。今回は、小売業における数年分の行動ログデータを分析に用いました。配布から1ヶ月の間が使用期限のクーポン施策が実施されたのはこのデータの最終年でした。クーポン施策以前のデータからSurrogate indexを推定し、その推定結果を実験データに活用してクーポン施策の長期的な効果を推定しました。
今回の分析では、長期指標 \(Y_i\) として長期間の週あたり平均購買額、中間変数 \(S_i\) として短期間の各週の購買額や来店頻度といったものを考えることができます。このような中間変数を用いた Surrogate index により、あるクーポン施策が長期的な購買額にどのように影響を及ぼすかを分析しました。
中間変数として用いるデータの期間を長くすると、長期的な処置効果の推定精度は傾向的には向上します。しかし、これには長期的な効果を推定するまで時間がかかるというトレードオフを伴います。
そこで、中間変数として処置後何週目までのデータを用いるか、その期間を変動させたもとで、長期処置効果の推定精度をナイーブな推定による推定値と比較検証しました。ナイーブな推定では、施策実施から経過週wまでの期間の週あたり平均購買額に対する平均処置効果を計算し、それを長期の週あたり平均購買額への平均処置効果の推定値としています。下図では、横軸が施策からの経過週w、縦軸がw週までのデータを用いた長期処置効果の推定値を、ナイーブな推定とSurrogate indexを用いた推定それぞれについてプロットしています。この図では例示のため、処置から23週間の間を長期としています。また、赤い水平線は真の長期的な処置効果の推定値を表します。
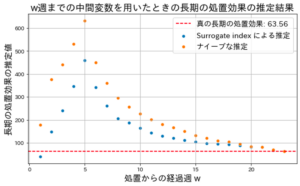
推定の結果、施策後どれほどの期間のデータを中間変数として用いても、今回の Surrogate index を用いたアプローチが長期的な効果をより正確に推定できることが確認できました。この結果から、短期的な処置効果と長期的な処置効果は同じとは限らず、短期的なデータをナイーブに活用してしまうと、施策の長期効果を大きく見誤ってしまうことがわかります。一方で、真の長期処置効果と Surrogate index による推定値の乖離はまだまだ大きいことも確認できました。この推定値の乖離は、インターンの時間の都合上、限られた種類の中間変数のみを用い、さらにSurrogate index の推定に単純な線形回帰を用いたことが原因だと考えられます。そのため、様々な中間変数を採用し、Surrogate indexの推定により柔軟なモデルを用いることで、推定精度の大幅な向上が期待できます。
Surrogate index を用いたアプローチではなぜ推定が改善されたのでしょうか？その理由は、施策が各中間指標をどの程度増加させ、その中間指標が長期指標をどの程度増加させるか、ということを定量的に表現できている点にあると考えられます。この点について説明するために、下に図を示します。この図は、施策開始から16週後までのデータを中間変数に用いたときの、経過週wにおける中間変数の重みを表しています。
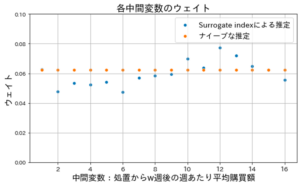
横軸が施策からの経過週wを表し、縦軸はナイーブな推定とSurrogate index による推定においてw週の中間変数にかかる係数（ウェイト）を表しています。ナイーブな推定では経過週wによらず固定値をとります。一方、Surrogate index による推定では、wが大きい、すなわち施策から時間が経過した週における中間指標（ここでは購買額）の係数が大きい傾向にあります。
これを購買行動の観点で解釈してみます。例えば、需要の先食いといった要因を考えると、クーポン施策は施策直後の購買額（中間変数）を大きく増加させても、それが長期的な購買額の増加につながらないことがしばしばあります。これは、Surrogate index においてwが小さい、すなわち施策直後の週の購買額にかかる係数が小さいことと対応しています。つまり、施策直後の購買額の増加が長期的な購買額を増加させる効果が小さいことを意味します。一方、施策からある程度時間が経った時期の購買額が高い顧客は、購買した小売店に定着していると解釈でき、その後長期間にわたる購買額が大きいと期待できます。そのため、施策から時間が経てば経つほど、その週の購買額の増加が長期的な購買額を増加させる効果が大きいと見込まれます。
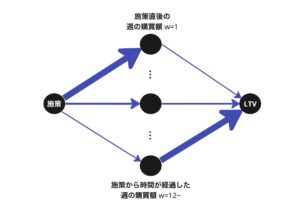
このように、Surrogate index を用いることで、施策が各中間指標をどの程度増加させ、その中間指標が長期指標をどの程度増加させるか、その効果の違いが定量的に考慮できていると考えられます。
最後に
私は計量経済学・産業組織論の分野に関心を持って大学で勉強・研究してきました。それらの知識がビジネス・実務の現場でどれほど活かせるか興味を持っていたところ、今回のチームにインターンシップ生として受け入れていただきました。手法のサーベイから始め、最新の論文を読み、実データへの応用まで行うという貴重な経験をさせていただけました。特に、研究の学術的新規性を既存文献の流れの中に位置付けるという目的ではなく、ビジネスでのデータ分析への応用を目的として論文を読むという経験は新鮮でした。
私自身、実データ分析を行う上で慣れない部分もありましたが、チームの皆さんの助けもあり楽しいインターンシップとなりました。この場を借りてチームの皆さんに感謝申し上げます。また、本記事の原稿を読んで詳細なコメントをくださった東京大学大学院経済学研究科の奥井先生、大学院生の方々にも感謝申し上げます。ここまでお読みいただきありがとうございました。
参考文献
Athey et al. The surrogate index: Combining short-term proxies to estimate long-term treatment effects more rapidly and precisely. No. w26463. National Bureau of Economic Research, 2019.
- 元論文では、共変量情報を用いたより一般の識別・推定方法や、Surrogate index 以外の形で中間変数を活用した識別・推定方法も議論しています。本稿では、推定量の単純化・直感的な説明のために、また、長期の処置効果推定を施策後短期間で行うという点に焦点を絞るために、処置がランダムに割り当てられている状況における Surrogate index を用いた識別・推定方法を紹介しています。また、元論文では Surrogate index による推定量の効率性についても議論していますが、本稿では割愛します。↩
- 元論文ではこの S のことを主にSurrogate variable (代理変数) と呼んでいますが、この S を中間変数、Surrogate index を Y の代理変数と呼ぶほうがより一般的だと考えたため、本稿では Surrogate variable を中間変数と表現しています。↩