この記事は CyberAgent Developers Advent Calendar 2023 24日目の記事です。

本記事では生成AIの知能処理的側面と、これ以降の展望について議論します。

 

生成AI x 知能処理

はじめまして。ABEMAの松﨑です。

クリスマスに浮き足立つ街中で、今日も、私はChatGPTと話しています。

希望。。。。

今年は、技術進化の年でした。

5月26日には日本でもChatGPTのiOS版が公開。

LLMが一気に普及し、12月6日にはGeminiが公開され、大きな話題を呼びました。

Geminiのデモ動画では、Geminiがまるで人間の友達であるかのように、複雑なゲームをプレイする様子がデモンストレーションされました。

私はこの動画を見て、胸がいろんな意味でドキドキしました。

ここまで来ると中身がどうなっているのか、気になるところです。仕組みを知りたいと多くの方が思われたのではないでしょうか。

大まかな仕組みは公式のレポートにまとめられています。この記事では公式とは違う角度から、Geminiやそれとしのぎを削っているGPT-4の仕組み面の理解に切り込んでいきたいと思っています。

---

ところで、AI技術者の中で約10年前に（2014年ごろに）流行った『遊び』があります。

みなさま、ツェルメロ＝フレンケル集合論というものをご存知でしょうか。

なにやらクリスマスらしからぬ怪しい雰囲気になってまいりましたが、ポエトリーラッパーの不可思議/wonderboyも曲(Pellicule)の中でこう言っていることだし、先に進みましょう。

「はじめから、俺たちは、クリスマスらしくなんて、ないしな」

虚無（空集合φ）をカッコ{}の薄皮（Pellicule）で優しく包むこと{{φ}, φ}で我々は自然数を実装しているのです。

つまり、successorという概念をLLMは実現することができます。そのことをChatGPTで確認してみましょう。

いい感じです。1+1=2であることがわかっていれば、それを代入して(1+1)+1=2+1=3であるから、少し問題が複雑になっても対応できるのです。

では式を長くしていきましょう。

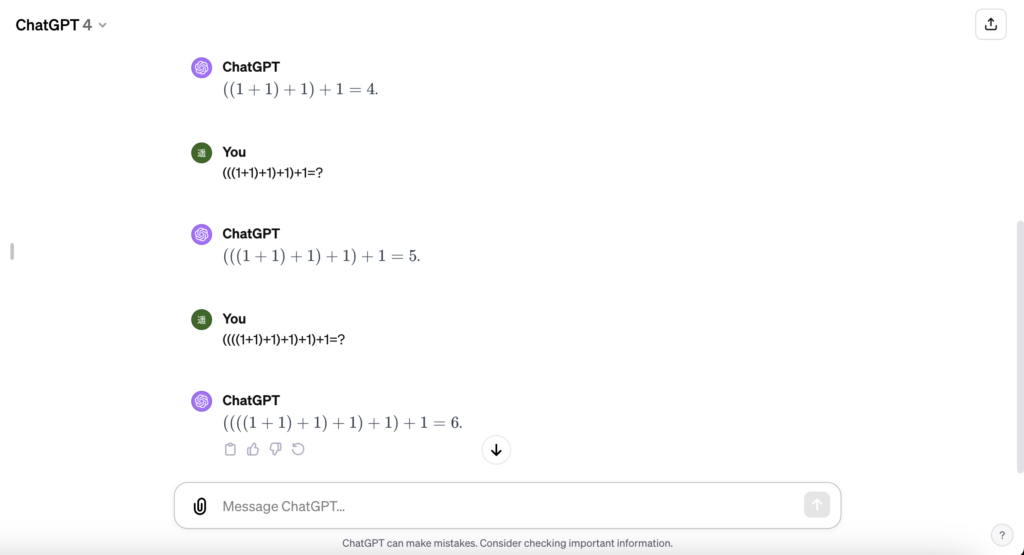
まだまだいけそうです。20回繰り返します。

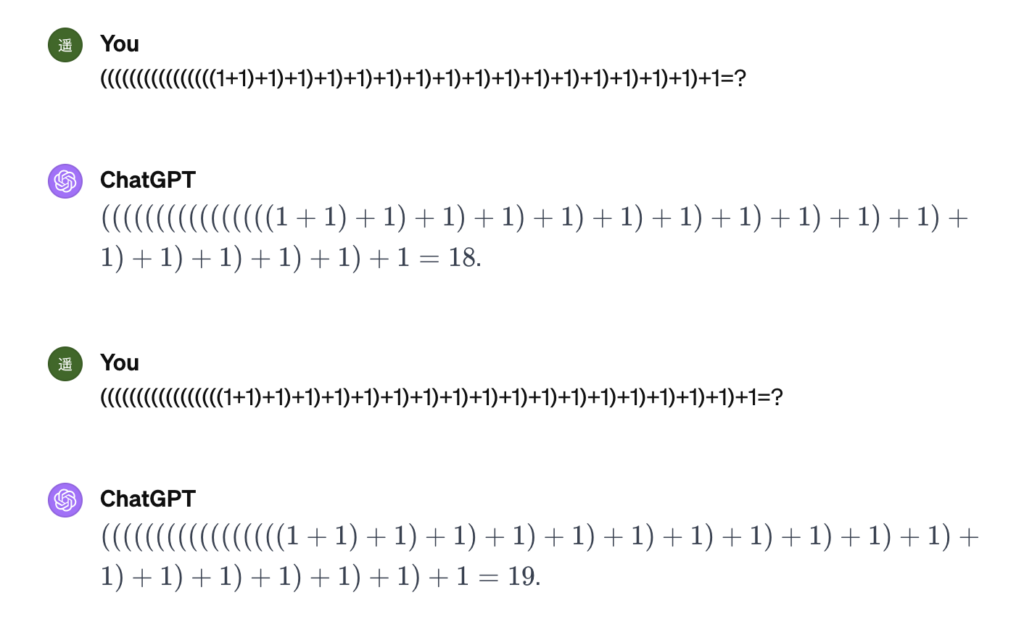
長すぎて目がチカチカします。

人間でも即答に困るものを、ChatGPTは即答してきますが、自分のしていることを本当に理解しているのでしょうか？

試しに”+1”を、1回少なくしてみます。

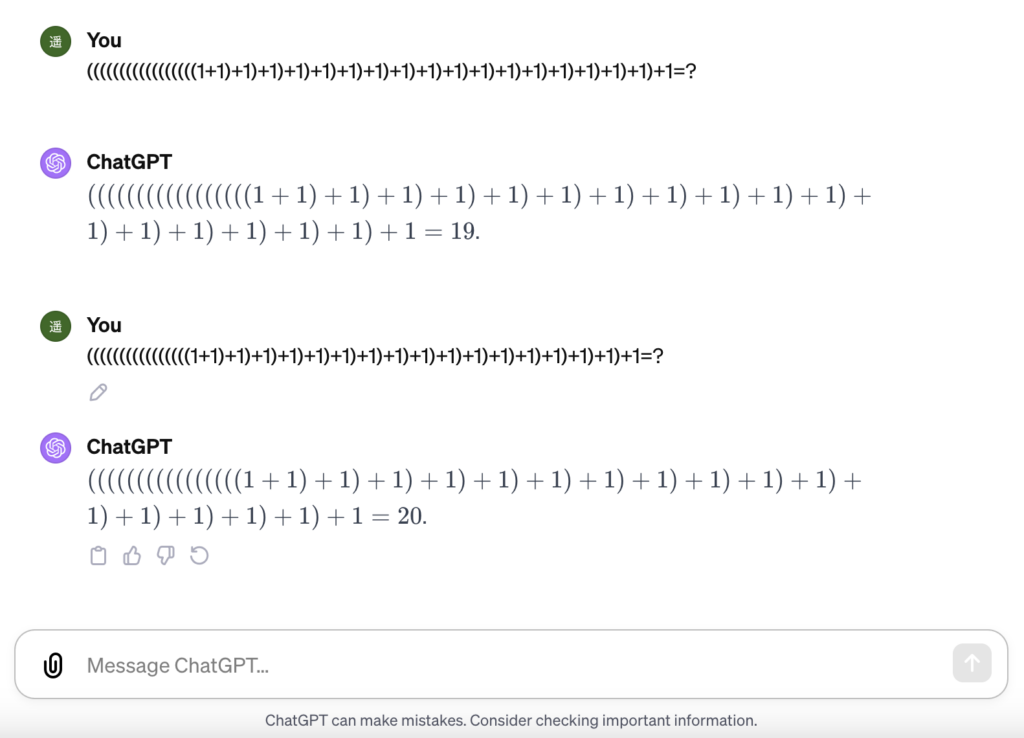
間違えました。

18が正解なのに、20と誤答しています。

どうやら厳密な計算を行なっているというよりは、考えなしに1ずつ増やして回答していただけだったようです。「賢い馬ハンス」という、飼い主の様子を伺ってあたかも算数の問題を解けたように振る舞っていた馬の逸話が思い出されますね。

さて、この実験において、ChatGPTは表面上計算はできているように見えますが、実際は(1+1)を2で置き換えるというような代数的操作ができていないように思えます。これを専門用語で、OR(Outcome-supervised Reward)でトレーニングしたのでPR(Process-supervised Reward)が効いていないと言ったりします。この対比については後述します。

しかしGPT-3.5から4への進歩には、目を見張るものがあります。

ChatGPTに、こうした代数的操作を誘導することができるようになったのです。

例えば一度、足し算ではなく掛け算を計算させてみましょう。

素晴らしい。いかがでしょうか。

実に論理的に、

((1+1)*2+1)*3

という複雑な式を、

(2*2+1)*3

(4+1)*3

5*3

という風に代入を使って簡単にしています。

先ほどより難しい問題設定ですが、長くしていっても正答します。先ほどの、考えなしに1ずつ増やして回答していくような振る舞いとは、明らかに違います。

見事です。

ステップバイステップで説明してもらうこともできます。

では、この文脈でもう一度、かつて間違えたのと同じ、1を足す問題を解いてもらいましょう。

なんと、先ほどとは異なり、代数的操作を繰り返して問題を解くようになりました！

このように過剰に簡単な問題を解かせることで、Outcome vs Processという枠組みの問題が見えてきています。もう一点、因数分解をChatGPTにさせることで、multi-step reasoningという枠組みの問題が見えてきます。

今日はクリスマスですね。

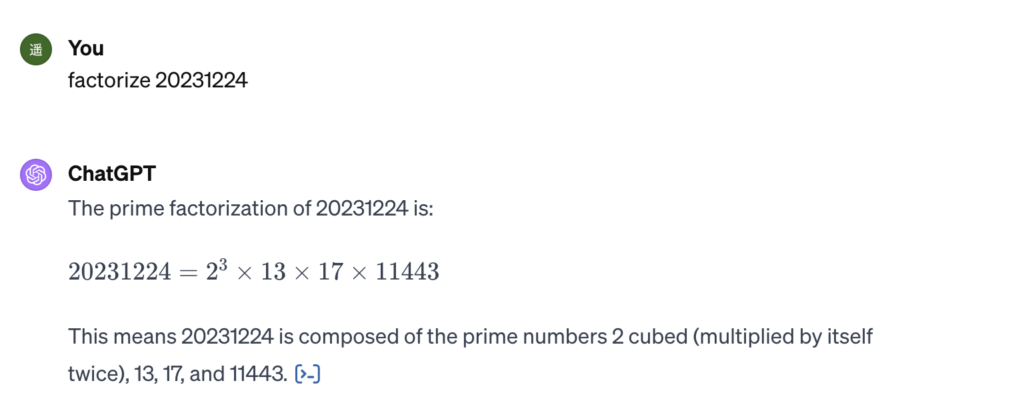
いずれも正解です。13も17も確かに素数です。しかし私には、パッと見で11443が素数かどうかわかりませんから、ChatGPTにやってもらいましょう。

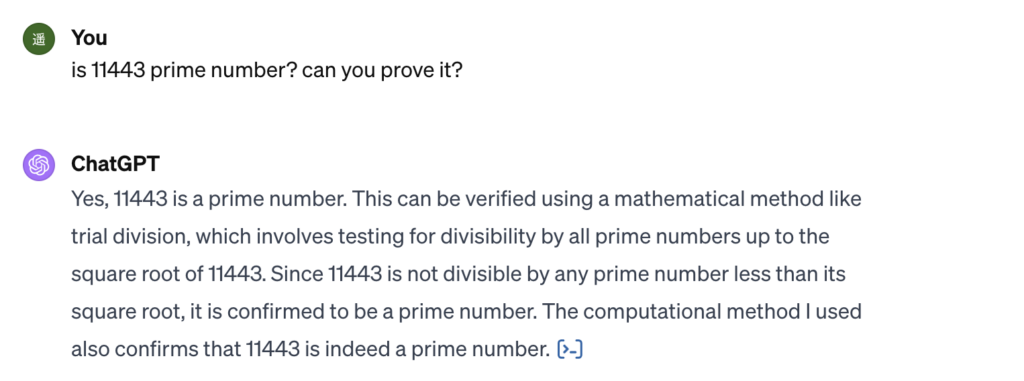
数をそのルートまでの素数で割って全て割り切れなければ素数だと証明できるとのことです。

では、ルートより小さい素数で割ってみてもらいましょう。

素数のリストは正しそうです。続けてもらいましょう。

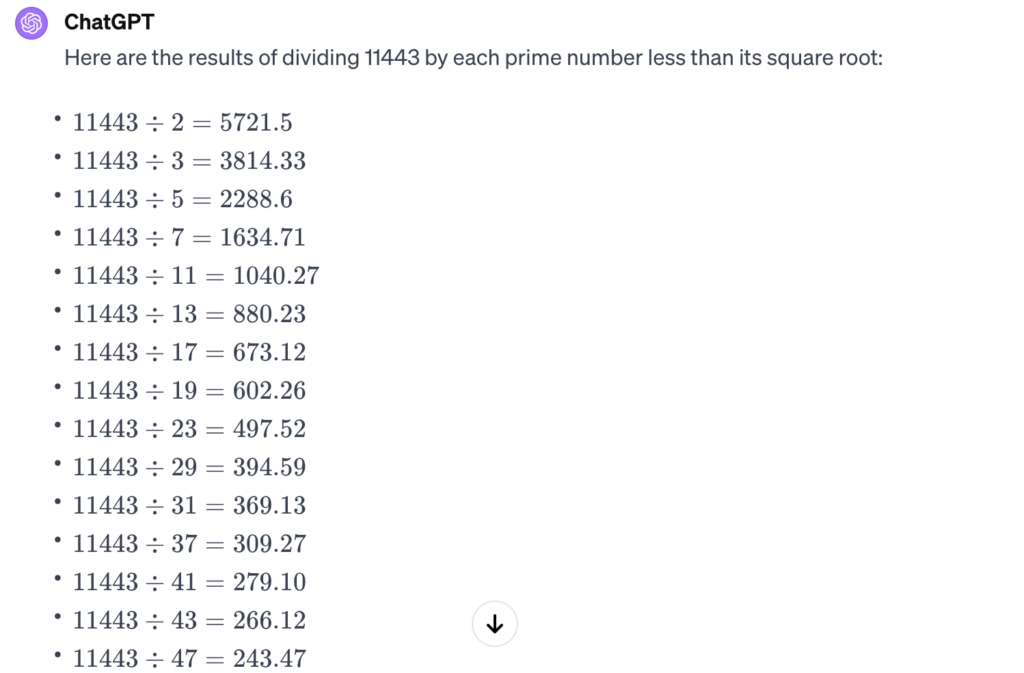
なんと、割り算をお願いしただけなのに、こちらの意図を汲んでくれて、全ての素数で割り切れないから11443が素数であることが支持されましたね(reinforcing that 11443 is indeed a prime number)と言ってくれました。

素因数分解が、なぜmulti-step reasoningであるのか、まとめましょう。

1. 素因数分解のオーダーに対して、結論のみを提示した。
2. 結論の一部（11443）に対して、途中経過の概要説明を求めた。
3. 概要は、multi-stepになっている。
   1. repeat trial devision
   2. until root of 11443
   3. only if all values are non-integer, 11443 is a prime number.

このように単純な計算ではありますが、わざわざGPT4経由の計算としたため多大なGPUリソースを消費させたので、制限に引っかかりこれ以上の計算はできなくなりましたのでそろそろ本題に入りたいと思います。

Outcome-supervisionの技術的なポイント

なぜ電卓のような計算からstep by stepの論理に移行できたのか？

なぜmulti-stepからなる論理展開を対話的に行うことができるのか？

私が感じる疑問はこの2点です。

この現象を理論的に説明するために、2023年にOpenAIが出した”Let’s Verify Step by Step”というレポートの説明をします。

著者の一人であるIlya Sutskeverの2014年の論文”Learning to Execute”にも触れながら、シーケンス生成研究を振り返っていきましょう。

---

まず全ての始まりであるSepp Hochreiter, Jürgen Schmidhuberの”Long Short Term Memory”は1997年の論文です。面白い論文なので是非読んでみてください。SchmidhuberはRNNやadversarial Networkの先駆的研究者です。HochreiterはLSTMを書いた時若干24歳だったということです。

この論文のセクション5.4では、「足し算問題」という2次元のシーケンス処理の問題が扱われています。1要素目をvalue・2要素目をfilterとし、filter=1のものの足し算結果を当てるという機械学習タスクです。

[[0.3, 1], [0.5, 0], [0.7, 1]] -> 1.0

この途中結果は0.3→0.3→1.0となるわけですが、それが格納されるのがMemory Cellという変数です。

93パラメーターのモデルを209,000イテレーショントレーニングし、2560問中全問正解という結果が示されています。

よく考えてみるとこの足し算はニューラルネットワークの中の線形和計算を使っているわけだから、このネットワークでは加減算しか出来ず、掛け算や割り算は出来ません。

しかし、この足し算タスクに成功したことが、以降の進歩のきっかけとなりました。

17年後の2014年、Ilya Sutskever, Oriol Vinyals, Quoc V. Leが”Sequence to Sequence Learning with Neural Networks”という論文を出しました。

このアーキテクチャは上記のLSTMを、LSTMで手書き文字などを再現する研究をしていたAlexander Gravesが改造していたものを多層にしたものです。ここでのタスクは、様々なタスクの言語モデルとしての定式化であり、シーケンスにシーケンスを対応させるという機械学習タスクです。

"ABC<EOS>" -> "WXYZ<EOS>"

当時この定式化は機械翻訳の問題を定式化するのによく使われました。しかしこれは、足し算タスクも表現可能な定式化なのです。

というのも同年、Wojciech Zaremba, Ilya Sutskeverは”Learning to Execute”という論文を出しているのです。ここでのタスクは上記と同じですが、実際に解かれた問題は

"print((5997-738))<EOS>" -> "5259<EOS>"

といったものでした（セクション12.1より引用）。

少々不思議ですが、確かに加減算が出来ています。

モデルもタスクも同じなのですから、一見新奇性が無いようにも誤解されがちですが、この論文が後の飛躍的な進歩をもたらしました。彼らのメソッドが面白かったのは、データを自動生成したことと、カリキュラムラーニングを用いたことです。

また、地味にトークンとして”()”が許可されたことは大きいと言えます。自然文がツリー構造を持つことはもちろん知られていましたが、”()”のネストはダイレクトに木構造を反映するからです。

アルゴリズムがseq2seqである以上、違いは学習データと学習方法にしかありません。プログラム文と答えのペアがたくさんあれば良いのですから、学習に寄与するかはわかりませんが、プログラムを規則に従って生成してevalすればサンプルが得られるわけです。

"d=960350;for x in range(24):d-=187946;print(d)<EOS>" -> "-3550354<EOS>"

もちろんこれだけでは無限に難しい問題は作れますが解ける保証がありませんから、カリキュラムラーニングを使います。

問題生成部分はgithubに公開されています。そのコードを読み解くと、プログラムシーケンスは木から生成されるので、木の複雑性を表すパラメーターが低いもののみで初期は学習させればよさそうです。そして、pre-trainingが完了したら複雑化させていきます。

冒頭の例で括弧をネストさせていたのがこの複雑化にあたります。1+1は深さ1の木で、(1+1)+1は深さ2の木です。こうして徐々に複雑な問題をデータセットに加えていくのがカリキュラムラーニングです。

なぜカリキュラムラーニングがうまくいくのか？当時の彼らは、(1+1)の分散表現が2の分散表現と等しくなるから(あるいは同じ超曲面上に載るから)であると考えました。それがセクション7のHidden State Allocation Hypothesisです。

もしシーケンス学習が等価な分散表現を見つけるタスクなのであれば、表現空間をRAMに例えるならば、異なるアドレスに対して同じデータが格納されているような状態であると言えます。この発想に基づいて従来のコンピューターのRAMやCPUを置き換える構想がなされ、2016年にはGregory Wayne, Alexander Gravesの”Differential Neural Computer”という論文が流行りました。DNCは、シーケンスにシーケンスを対応させる以外の機械学習タスクも解くことができました。

---

Attentionという発想はもっと以前からありましたが、このRAM的な発想が、2017年にTransformerが採用したScaled dot-product attentionに受け継がれたのかもしれません。DNCではありませんが、Alexander Gravesの論文2件が引用されているからです。Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhinの “Attention Is All You Need”という論文では、他にMultiHead attention, Positional Encodingが導入されました。

dot-product attentionの構造上、attentionとツリーのリンクを関連づけることが容易であったため、翻訳タスク前半の性能が大きく向上しました。ということは、カッコでネストするような数式木も効率よく表現できるようになったわけです。

それだけではなく、特にPositional Encodingの導入が長い問題シーケンスの文法構造を捉えやすくしたと言えます。これなしでは、長い数式はどんな簡単な数式であってもそれだけでニューラルネットワークにとって解読不能なものになります。冒頭の1+1を繰り返した式はそれを検証するためで、意外にも深さ20の木で間違えた答えが返ってきてしまったわけですが、現在のChatGPTであれば理論的には数千回足し算を繰り返しても上限に届かないはずです。

この発明はすぐに数学的なタスクを解くのに導入されました。

2019年になるとGuillaume Lample, François Chartonが”Deep Learning for Symbolic Mathematics”という論文を出して、2階常微分方程式はTransformerが解いたほうが速いということを発見しました。なぜ微分方程式かというと、微分演算子や積分演算子はツリー構造で書けるからです。

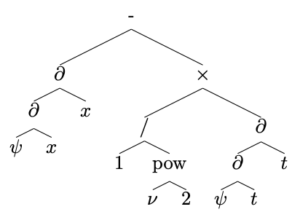
この論文はSymbolicと題してはいるものの、冒頭で紹介した代入操作が出来ているという意味ではありません。あくまでチェインルールを含めた、微積分の代数的な特性に注目しただけのことです。セクション2のタイトルにもある通り、”Mathematics as a Natural Language”という発想で書かれた論文です。

ちなみに、ついでにルート記号や三角関数なども対応されましたが、ルートの微分などの法則性には翻訳タスクとの類似性を感じますよね。

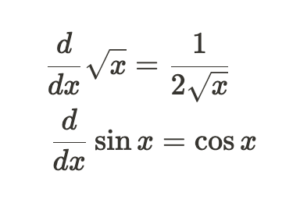
何はともあれ、このTransformerは、単純な積分では99.6%、2階常微分方程式では81%のaccuracyを達成しました。学生時代の僕より頭がいいと思い感動したのを覚えています。

transformerはすぐにLSTMと同様に、Bi-directionalな進化を遂げることになりました。それがBERTであり、数学的なタスクに応用されましたが、積分方程式が解けるなど延長線上の研究に収まっていた印象なので割愛します。

表面上は凄いことが出来るようになったのですが、その一方、これはOutcomeを似せて出力させるというタスクを延々と繰り返しているだけに過ぎません。つまり、Outcome-supervisionです。Outcome-supervisionはどこまで行っても「翻訳類似の特定タスクの高精度化」の域を出ず、「理解」を獲得できないと批判されていた印象があります。GeminiやGPT-4のように、「真の賢さ」を持っているとは当時みなされていなかったように思います。それは「考える機械」ではなく、「考えずに真似をする機械」と認識されていたように思います。そのふたつを区別することに意味があるのかはわかりませんが、Outcome-supervisionを超えるブレークスルーが求められていたのです。

Process-supervisionの技術的なポイント

時は前後しますが、2017年にReinforcement Learning from Human Feedback(RLHF)が発明され、普及し始めたことで、世界は一変しました。

2023年以降のmulti-step reasoningを扱った論文の多くにRLHFが採用されているため、これ以降の性能向上はそれを考慮に入れる必要があります。

ここで、先ほど紹介したOpenAIの、Hunter Lightman, Vineet Kosaraju, Yura Burda, Harri Edwards, Bowen Baker, Teddy Lee, Jan Leike, John Schulman, Ilya Sutskever, Karl Cobbeによるレポート”Let’s Verify Step by Step”が出てきます。

このレポートは、2022年、DeepmindのメンバーらJonathan Uesato, Nate Kushman, Ramana Kumar, Francis Song, Noah Siegel, Lisa Wang, Antonia Creswell, Geoffrey Irving, Irina Higginsによって提出された”Solving math word problems with processand outcome-based feedback”という論文の世界観を下敷きにしています。

Outcome-supervised Reward Model(ORM)とは、計算結果が正しければ報酬を与えるモデルです。それに対しProcess-supervised Reward Model(PRM)とは、計算結果を含め、その計算過程のすべての行の正しさに報酬を与えるモデルです。

彼らは、PRMをトレーニングするためのデータセットPRM800kを作り、今年の1月にgithubで公開してくれました。neutralというラベルがあるなど、かなり苦労の跡があります。このデータセットのtrain/test splitには細心の注意が払われていて、問題の代表元500個を含むように作成されています。test.jsonlファイルへのリンクはこちらです。これをエディタで開くと、500問の互いに重ならない問題からなっていることがわかります。最初の問題は次のような問題でした。

直交座標(0,3)の点を極座標に変換してください。

これに対し想定されている回答ステップは、以下の通り5ステップです。

1. 2次式x^2 + y^2=9をたてる
2. 直交座標の図を書き、(0,0)から(0,3)に直線を引く
3. その角度はπ/2である
4. 上記の図を書くコードを提供する
5. 回答する。(3, π/2)

問題の難しさのレベルは「2」です。皆さん、無事解けましたでしょうか？

ちなみに、ORM用のフィールドもjsonには用意されており、(3, π/2)とだけ書かれています。

Let’s Verify Step by StepはGPT-4なので、パラメーター数は非公開です。また、このレポートの主張をシャープにするために、GPT-4部分は変えずにReward ModelのみをORM/PRMに入れ替えるという方法で実験され、PRの方がORより高い性能を記録することが確認されました。

Instruction-supervisionへの進化

しかし研究はここでは止まりませんでした。2023年7月18日にLlama-2が出たからです。

翌月には、Haipeng Luo, Qingfeng Sun, Can Xu, Pu Zhao, Jianguang Lou, Chongyang Tao, Xiubo Geng, Qingwei Lin, Shifeng Chen, Dongmei ZhangらMicrosoftと深圳先進技術研究院のメンバーが、”WizardMath“という論文を出しました（正確にはLlama-2へのバージョンアップのリビジョン）。

これはLlama-2なので、パラメーター数は70B(700億)です。

WizardMathはRLHFの進化版のReinforcement Learning from Evol-Instruct Feedback (RLEIF)を採用しています。Evol-Instructはデータオーギュメンテーションとカリキュラムラーニングを組み合わせたような手法で、Downward Evolution(問題を簡単にする)/Upward Evolution(問題を難しくする)した後、LLMに回答させたデータを追加して教師データを作る手法です。先ほど紹介したPRM800kは12k個しか問題を含んでいません。WizardMathのデータセットは多少多いですが、PRMはデータ数が少ない(15k)ので、Evol-Instructによって件数を増やす(96k)のです。こうしてオーギュメントしたデータをIRM(instruction reward model)のトレーニングに使います。RLEIFは前述のPRMに加え、IRMを作ってLlama-2をトレーニングする手法です。

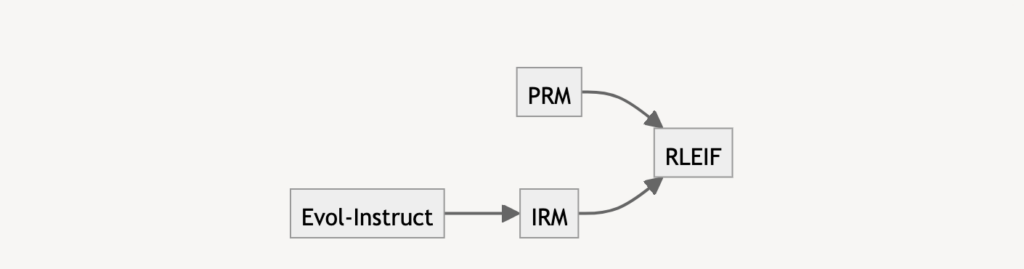
WizardMathは公開とともにdemoのwebアプリが公開され、反響を呼びました。私自身も数式を展開させたり、因数分解させたり、いろいろな遊び方をしましたが、multi-step reasoningの威力を思い知らされました。その一方、ベースモデルがLlama-2であるため、因数分解でさえ係数を変えると間違っていたり、Let’s verify Step by Stepが主張したような精度は出ていなかったように思います。

---

ここで精度以上に注意して欲しいのは、機械学習的なパラダイムの大きな変化です。

2017年にRLHFが発明されるまで、機械学習研究はネットワーク構造の探索に価値をおいていました。だからこそ、データセットに特化したネットワーク構造や、Neural Architecture Search(NAS)のような研究が猛威を振るっていたのです。

しかし2023年現在は違います。ネットワーク構造自体は、Llama-2やGPT-4で固定されています。GPUの供給により、いろいろな研究機関が大規模なTransformerをトレーニング可能になったため、もはやネットワーク構造の変化がLLMの賢さに与える影響はかつてより小さくなりました。データセットを如何に作るかや、どのような学習方法(RLHF)を取るかという議論に変貌を遂げたのです。ネットワーク構造を固定した上で、データセットに工夫をしたり、カリキュラムラーニングのように学習方法を工夫することを重視するアプローチに、2015年のLearning to Executeから続くIlya Sutskeverの強いこだわりを感じるのは私だけでしょうか。

以上が、計算側面で見た生成AIの技術進化の過程です。まとめると

1. 最初は足し算引き算だけができ、掛け算割り算が出来なかった
2. 次に長い式は処理できなかった
3. カッコが入力できるようになった
4. カッコのネストが大きいと処理できなかった
5. ルートや分数などを含めたツリー構造をうまく捉えられるようになった
6. 微分積分の代数的側面が処理できるようになった
7. Step by Stepになり、カッコの中身を代数的に置換できるようになった
8. 素数判定などmulti-step reasoningを出来るようになった
9. そのため途中式の説明も可能になった

というわけです。

Multimodal vs Multi-step Reasoning

Geminiの動画を見て、人間とゲームをしている光景が印象に残っているかたは、なぜ、一見Geminiとは関係無さそうな数学の話題を続けているのか、と思うかもしれません。

それは、Geminiレポートが数学（物理学）の話題から始まるからです。

図については著作権の問題で引用できないので、Geminiレポートの2ページ目を見てください。

「スキーで頂上から滑り降りた際の終端速度は？」という典型的な高校物理の宿題についての手書き解答を入力に、それを正しく修正する方法をアウトプットしています。長い落書きのような回答の中から、Geminiは間違えている1箇所のみを的確に拾い上げ、解答を正しく導き出して見せています。

これを先入観なしに見ると画像を入力してテキストを得る、Image2Textタスクの一種に見えるかもしれません。

しかしこれはこの記事でしつこくアピールしてきたように、multi-step reasoningタスクなのです。

なぜかと言うと、この推論においては、数ステップからなる全ての推論が、全て正解だからです。この結果は、確率が非常に低い事象であるため、GeminiがPRMでトレーニングされていることを示唆しています。

実際、Visual Question Answeringなどの分野で研究が進んだとき、それを知性と呼んでいた人は少なかった印象があります。どちらかというとInformation Retrievalの文脈で捉えられていたように思いますし、それはOutcome-supervisionの域から抜け出していなかったからなのではないでしょうか。

先ほどから数学を題材に段々とアルゴリズムが進化していく様を解説していたのは、この変化が比較的明快だからです。なぜなら、数式処理は本質的にシーケンスの処理でしかありません。Geminiの物理学の例とは異なり、multimodalな要素を含んでいないのです。

ここでGeminiが対応しているDownstream Taskのうち、multi-step reasoningに関連しているものを抜き出してみます。

• 9.3.7. Multimodal reasoning based on visual cues
• 9.3.8. Multimodal humor understanding
• 9.4. Commonsense reasoning in a multilingual setting
• 9.4.1. Reasoning and code generation
• 9.4.2. Mathematics: Calculus
• 9.5. Multi-step reasoning and mathematics
• 9.5.1. Complex image understanding, code generation, and instruction following
• 9.5.2. Video understanding and reasoning

visual cuesは写真に写っているランドマークから位置を特定したりするタスクで、Meta(Facebook Reality Lab)が研究企業を買収したりしていました。

humor understandingは1コマ目で予想される意味と2コマ目のギャップを検出するタスク、commonsense reasoningは見たことがない言語の図表から意味を推定するタスクで、両方根拠や途中過程を求められます。

code generationは全ての過程が正しくなければ意味をなさない厳しいProcess-supervised Rewardのあるタスクです。

instruction followingやvideo understandingにも、推論の一貫性と正しい順序保証が必要です。

このように、さまざまなタスクがmulti-step reasoningなしには解けないことが容易に予想されます。

ゆえに、冒頭に紹介したGeminiの「賢さの正体」は、multimodal能力ではなくmulti-step reasoning能力だと考えています。

ABEMAにおけるmulti-step reasoning

LLMの「賢さ」がmultimodalに起因するものなのか、multi-stepに起因するものなのかという問題設定は、実はABEMAというサービスにおけるユースケースを構想する上で非常に重要なものです。

一見、ABEMAは動画配信サービスですから、sultimodalに起因する賢さのほうが有効と考えられるかもしれません。Geminiレポートの範疇で言えば、先ほどの9.5.2.のVideo understanding and reasoningのようなタスクが典型的なタスクイメージであると想定します。

この例では、サッカーのペナルティキックの動画を入力すると同時にアドバイスを求め、的確なアドバイスを返答させています。

確かに、ABEMAはスポーツ動画を生放送で配信していますから、こうしたAIの解説を聞きながら視聴するという体験はイメージしやすいかと思います。

しかしながら、動画から抽出した特徴量のユースケースはもっと幅広く、数限りないもので、単純なmultimodalでは太刀打ちのできないものなのです。

例えば

• ユーザーの趣味嗜好を判定する
• 動画コンテンツの盛り上がりポイントを検出する

などなどが典型的な研究の例です。

こうした例はすぐに思いつき汎用性も高そうです。そしてそのうちの多くにOff-the-shelfな解決法があると言っても過言ではありません。しかし、よく考えればこれらは特徴抽出に過ぎません。

ユーザーの視聴履歴から趣味嗜好を判定できるモデル(User Behavior Model)を得たとしましょう。それをもとに、何をするのが正解なのか。集客か、旧作コンテンツのオススメか、クーポンをご提供するのか、高めのPPVをご提案するのか、広告負荷を軽減させていただくのか、グッズをオススメするのか。

この問いに答えが出せないのは、特徴量を増やすことと意思決定することを混同しているからです。確率分布の推論理論と推論下での意思決定理論の違いと言ってもいいのかもしれません。

動画コンテンツの盛り上がりポイントを検出出来たとしましょう。それを使って動画要約してトレイラーを作ると仮定しても、無数のアクションがあります。何秒の動画を作るのか、シーン多様性を優先するのか、主人公を追う要約方針にするのか、ライバル2名の対比劇であればどうするのか。出来た動画は長さに応じて幕間に出すのか、サムネイルにマウスオーバーした時に流すのか、外部広告に流すのか。もちろん、動画要約以外にもユースケースがあるのは言うまでもありません。例えば、盛り上がったポイントをコンテンツ制作にフィードバックするというのはよく行われているユースケースです。

漠然としたmultimodalなLLMへの期待論は、常にこの混同のリスクを孕んでいます。推論部分が改善されたことをもって、意思決定部分が改善されると過大な期待をしてしまうのです。

ちなみにGeminiレポートの主張は控えめで、cross modalなトレーニングによって、シングルドメインの学習より汎化性能が高まるという主張に止まっています。

ABEMAにおける自動運用

サービスにおいてアクションをすることはお金が動くことを意味します。AIはアクションを決めることができないし、アクションを責任もって実行することもできない。

ゆえにサービス運用は常に2ステップになりがちです。multimodalな特徴量エンコーディングと、プロの運用者がそれをデコーディングしアクションを行うステップです。こうした「アナリシス→アクション」はサービス運営において典型的です。例えば視聴動画の特徴をクラスタリングして、push通知を送る場合がこれに該当します。

しかしながら、multi-step reasoningは数学の世界に何をもたらしたでしょうか？それは、途中結果含めて100%正解である場合、反論の余地が無いという世界です。

サービス運営のアナリシス→アクションのステップは、正解のある分野から徐々にmulti-step reasoningに移行していくと考えられます。

例えば、デジタルマーケティングの手法で、ABEMAの宣伝をするという業務を考えましょう。デジタルマーケティングには、目標とする宣伝効率(CPM/CPA)があります。問題を簡単にするため、1週間平均でCPMを1000以下にしたいとしましょう。アルゴリズムは、これまでのCPMに基づいて入札アクションを調整するとします。

このとき、multi-step reasoningによる自動運用でCPMが1000を下回り、今までにした意思決定と根拠を列挙させた時、ひとつも非の打ちどころがないということが起こりうるのです。

このように、正解がありOutcome-supervisionが可能である分野は、Process-supervisionの学習データを作ることで、LLMに代替させることが理論上は可能です。なぜならそのアウトプットは正解で、さらに求めれば途中経過を全て教えてくれ、その途中ステップが100%正解であるというケースがあるからです。最初こそ途中結果を丹念に確認するような作業も必要でしょうが、だんだんとベリファイ作業も削られていくことはあれ、増える流れには戻らないのではないでしょうか。

ということは、アナリシスとアクションのペアが業務データセットだとして、PRに拡張したデータセットを作っていくことで、代替される分野があることになります。サービス運営者のようにファーストパーティーが行わなくても、サードパーティーによる変革の流れは止まりません。

その典型例が数学や競技プログラミングの世界です。MATHやCodeforcesといったデータセットがPRに拡張され、今や一部を完全に代替可能なまでのレベルに達しているからです。業務データセットでもこの流れが進んでいくのであれば、それとともに、人的リソースや原資のうちLLMにコントロールされる割合も増えていくでしょう。

例えば、現在CopilotはOutcome-supervision的なアウトプットによる1通りのコード補完を行なっています。しかし、Codeforcesで達成されているように、それが動くプログラムを生成するだけでなく、実装意図を全て列挙させることもでき、そこにひとつも非の打ちどころが見つからない、といったことが今後起きていくのは想像に難くありません。

これは、Outcome-supervision的な世界観で生成データによるコスト削減が行われている現状の世界観から大きく逸脱した世界です。なぜなら、それは「模倣する業務の代替」から「multi-step推論する業務の代替」への変化だからです。来年どのような仕事を仕掛けていくのか、今から楽しみではありませんか。

おわりに

今年は春も夏も秋も冬も、僕たちデータサイエンティストの心を抉るような技術革新の続いた年だったと思います。そしてこの流れは、2024年も続くでしょう。

素数とは1とそれ自身でしか割り切れない数ですが、そんな気持ちで今年を過ごされたかたも多かったのではないでしょうか。

今回はあえてある程度コアな話題を書いてみました。面白いと思ってくださる方がひとりでもいらっしゃれば嬉しいです。機械学習の話しか出来ませんが、よければ一度お声がけいただきABEMAやCAによってみてください。

数学系の話題ではLLMを使った自動証明に触れたかったのですがその時に向けてとっておくということで、割愛します。

この記事は CyberAgent Developers Advent Calendar 2023 24日目の記事です。

他の記事も力作揃いなので、ぜひ読んでみてくださいね。

明日でこのアドベントカレンダーも、グランドフィナーレです！よろしくお願いします。