こんにちは。協業リテールメディアdivでデータサイエンティスト、プロダクトマネージャーをしております早川です。本日はABテストにまつわるトピックを紹介します。

はじめに

とあるマーケティングコミュニケーションを介入とみなしたとき、一つの介入が異質性を持っていたり、複数のアウトカムに影響を及ぼすことは容易に考えられます。例えば缶ビールのクーポンを配布して、各消費者の缶ビールの平均購買点数が増えるかを検証する状況を考えます。このとき、ビールを好む消費者の購買点数が増えた、普段飲酒をしない消費者の購買点数は0本のままで影響がなかった、という状況が直感的に想像がつきます（異質性）。また、ビールの購買点数に加えて、おつまみ類の購買点数も増えるかもしれません（複数アウトカムへの影響）。

この介入の効果検証をABテストを通じて行うとき、異質性や複数アウトカムへの変化を含む、なるべく多くの変化を正確に捉えるにはどうするべきでしょうか。一つの実験で、複数のアウトカムや、複数のユーザのサブグループを同時に検証すると、いわゆる検定の多重性の問題が生じます。先の例において、例えば消費者を居住している都道府県別に分けてそれぞれの都道府県で効果があったかを統計的仮説検定で検証するとき、全く効果がない場合でも有意差があると判断される、偽陽性の状態になる可能性が有意水準0.05において91%におよびます。*1

検定の多重性への対応策としてボンフェローニの方法やホルムの方法などの事後的な対応方法をとることは可能です。一方で本ブログでは、偽陽性を小さくできるように事前に実験設計に手を加えられないか？ということを考えてみたいと思います。

代表的な方法として ①層化抽出②再ランダム化の2つが知られています。特に再ランダム化はここ数年で統計分野の論文誌等で改めて着目されており技術的な発展が見られます。幸い我々の実務における状況としては、実験設計そのものを工夫するコスト（ビジネス的な調整等のコストを含む）は高くなかったこともありこうした方法の検討をする余裕がありました。

今回は記事を2回に分け、これらの手法を、数式と簡単な数値実験を通じて紹介します。

第1回（今回）では共変量バランスを保つことで偽陽性を減らすアイデアについて焦点をあて、その方法層化抽出と再ランダム化の基本的な説明を実施します。

第2回では特に発展が見られる再ランダム化の手法について深堀りする形で紹介します。

共変量バランスを保ち、偽陽性を減らす

「偽陽性を減らす」を噛み砕いて表現するとノイズ（ランダムなばらつき）によって発生するデータの大小を、シグナル（本来検出したい効果）として誤って解釈しないようにする、と言えるかもしれません。例えば性別や年齢や過去の来店頻度といった共変量（特徴量）*2 の分布がトリートメント群とコントロール群で大きく異なるときにノイズが大きくなってしまうというのは直感的です。

この直感をもう少しだけテクニカルに議論するため、[Deaton and Cartwright, 2018] を参考に、以下のモデルを導入しましょう。

\[Y_i = \beta_i T_i + \Sigma_{j=1}^{J} \gamma_j x_{i, j}\]

ここで \(Y_i\)はユーザ \(i\) のアウトカム（例えばある商品の購買金額） \(T_i \in \{0, 1\}\)は介入（例えばクーポン）の有無を示すダミー変数。 \(\beta_i\)はユーザ \(i\)に固有の介入効果。 \(x_{i,j}\)はユーザ \(i\)の \(j\)番目の共変量（例えば性別、年齢、過去の来店頻度）で, \(\gamma_j\)は共変量 \(x_{i, j}\)がアウトカムに与える線形の影響を示しています。

\(T_i = 1\) であるトリートメント群のアウトカム平均を \(\bar{Y_T}\)、 \(T_i = 0\) であるコントロール群のアウトカム平均を \(\bar{Y_C}\)とすると、アウトカムの平均の差分は以下のように表現できます。

\[\bar{Y}_T – \bar{Y}_C = \bar{\beta} T + \sum_{j=1}^{J} \gamma_j ((\bar{x}_{T, j} – \bar{x}_{C, j}))\]

右辺の第一項はトリートメント群における介入効果の平均を示しており、検出したい「シグナル」に当たります。第二項は各群の共変量の差分による影響を示しており、差として検出したくない「ノイズ」部分だと言えます。トリートメント群とコントロール群で共変量分布をなるべく揃えることで、ノイズを小さくし、シグナルを正確に捉えることができることがわかります。実際に上記の数式に従って生成されたデータによるシミュレーションを考えます。

簡単のために \(\beta_i = 0\)を仮定します。これは「シグナル」となる介入の効果がない状況を考えることに相当します。\(x_{i,j}\)や \(\gamma_j\)は標準正規分布から生成します。


import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats

# データ生成
def generate_data(
    seed=0,
    N=1000,  # サンプルサイズ
    J=5,  # 特徴量次元
    K=3,  # 特徴量のうちバイナリなものの次元
):
    np.random.seed(seed)
    
    X_bin = np.random.choice([0, 1], size=(N, K))
    X_con = np.random.normal(size=(N, J - K))
    X = np.concatenate([X_bin, X_con], axis=1)
    
    beta = 0,

    gamma = np.random.normal(size=J)
    T = np.concatenate([np.ones(N // 2), np.zeros(N - N // 2)])
    Y = beta * T + np.dot(X, gamma) + np.random.normal(size=N)
    return X, Y, T

# トリートメント群とコントロール群の共変量の分布を比較
X, Y, T = generate_data()
fig, axes = plt.subplots(1, J, figsize=(5 * J, 5))
for j, ax in enumerate(axes):
    sns.histplot(X[T == 1, j], ax=ax, label="treatment")
    sns.histplot(X[T == 0, j], ax=ax, label="control")
    ax.set_title(f"x$_{{i,{j}}}$")
    ax.legend()

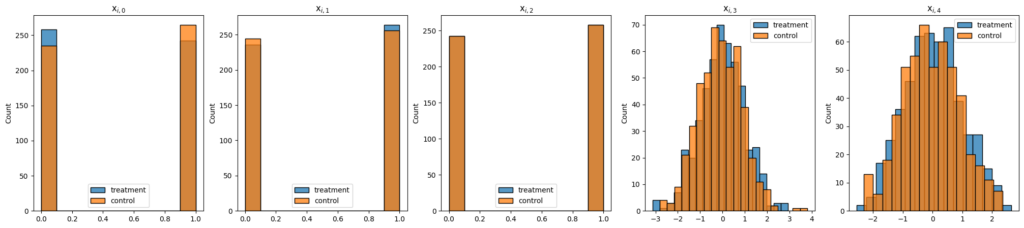
上記のコードを実行すると、トリートメント群とコントロール群の共変量の分布が少しずつ異なることがわかります。

これがどの程度の影響を与えるのでしょうか？

100回のシミュレーションを行い、Yの平均の差分についてp値を計算してみます。なお、ここではランダム化推論（randomization inference, Fisher’s randomization test）による検定を行っています。

ランダム化推論を採用するのは、いわゆる母集団からのサンプリングに基づく方法が、（後半紹介する）再ランダム化後の検定において推定標準誤差を増加させることが知られているためです。多くの再ランダム化を扱う論文でランダム化推論の使用が推奨されています [Morgan and Rubin 2015] [Johansson et, al. 2021] [Zhu and Liu 2023]

ランダム化推論については [Cunningham 2021] や[Imbens and Rubin 2015]などを参照してください。

p_values = []
for i in range(100):
    X, Y, T = generate_data(seed=i)
    t, p = stats.ttest_ind(Y[T == 1], Y[T == 0])
    p_values.append(p)

plt.figure()
sns.histplot(p_values, bins=20)
plt.title("p-value distribution")
plt.gca().patches[0].set_facecolor("orange")
plt.xlim(0, 1)

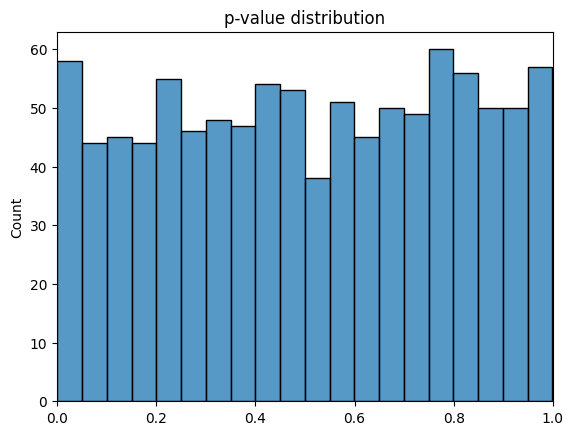
プログラムを実行することでp値の分布が得られました。0.05を下回るp値も全体の約5%の試行で観測されたことがわかります。実際に差がなくとも、共変量の違いの影響によって偽陽性が発生するケースがあることがわかります。

層化抽出による共変量バランスの保持

層化抽出は共変量の分布が異なるサブグループを作成し、それぞれのサブグループにおいてトリートメント群とコントロール群の割合を揃える方法です。

例えば、居住都道府県が共変量の一つである場合、居住都道府県ごとにデータを分割しそれぞれトリートメント群とコントロール群の割合を揃えるとします。この状況では \( x_{i,\mathrm{isTokyo}} \in \{0, 1\} \) をユーザ \(i\) が東京に居住しているかを示すダミー変数とすると、 \( (\bar{x}_{T, \mathrm{isTokyo}} – \bar{x}_{C, \mathrm{isTokyo}}) = 0 \)が言えるでしょう。

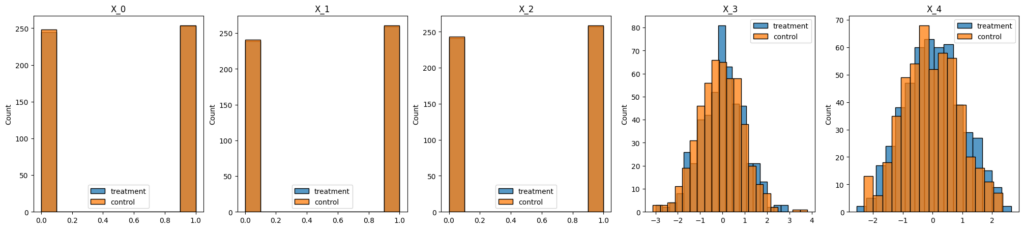
このように層化抽出を行うことで共変量バランスを保つことができ、特にその共変量がアウトカムに影響を与える場合に有効です。実装は割愛しますが、先ほどのデータ生成例にX_0, X_1, X_2について層化抽出を行った場合、X_0からX_2のバランスが取れていることがわかります。

再ランダム化による共変量バランスの保持

アウトカムに影響を与える可能性がある共変量全てで層化抽出を行うのは難しい場合があります。このような場合に再ランダム化は有効です。

再ランダム化のプロセスを理解するため [Morgan and Rubin, 2012]の画像を引用します。

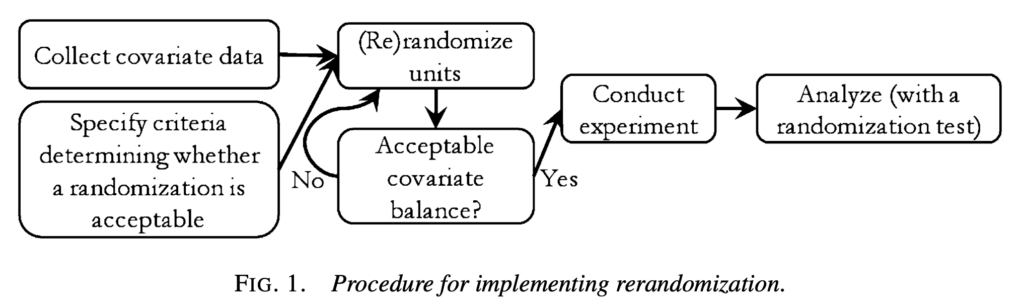
トリートメント群とコントロール群の共変量平均の距離についてある閾値を設け、その閾値を下回るまでランダム化をやり直すというわけです。[Morgan and Rubin, 2012]も含め、Rerandomizationに関する研究では以下で定義されるマハラノビス距離*3が距離基準として採用されることが多いです。

\[
M = (\boldsymbol{x}_T – \boldsymbol{x}_C)^T \mathrm{cov}(\boldsymbol{x})^{-1} (\boldsymbol{x}_T – \boldsymbol{x}_C)
\]

ここで \( \boldsymbol{x}_T, \boldsymbol{x}_C \in \mathbb{R}^J\) はそれぞれトリートメント群とコントロール群の共変量の平均ベクトル、 \(\mathrm{cov}(\boldsymbol{x})\) はデータセット全体の共変量の共分散行列です。

この \(M\) がある閾値以下になるまで、トリートメント群とコントロール群を割り付けし直す、まさにサイコロを振り直す、というのが再ランダム化の基本的なアイデアです。

簡単な数値実験

層化抽出と再ランダム化によって共変量のバランスが小さくなることを数値実験で確認してみましょう。

先ほどのデータ生成過程で乱数シードを変えながら1000回データ生成を繰り返し、共変量のバランスがどれくらい保たれるのかを確認したいと思います。共変量のバランスには上記で定義したマハラノビス距離を採用します。

比較手法は以下の3つです。

通常のランダム化（rct）
X_0, X_1, X_2について層化抽出（stratified）
閾値を0.05にした再ランダム化（rerandomize）

1000回データ生成を繰り返して手に入った1000個ずつのマハラノビス距離をヒストグラムとして描画すると以下のようになりました。

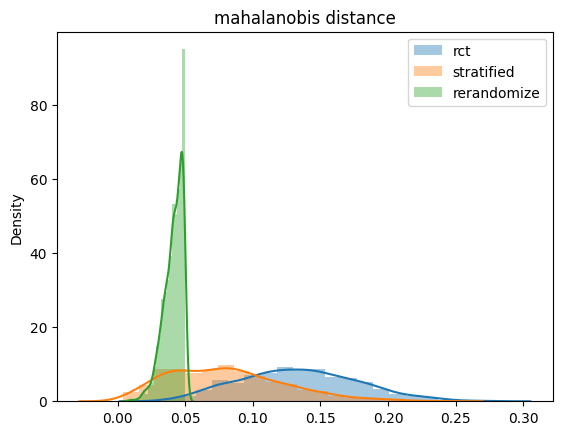
グラフは横軸に距離をとっており、これが0に近ければ近いほど共変量の差分がない、ということになります。まず、通常のランダム化（rct）は0.10から0.15あたりにピークがあり、層化抽出（stratified）は0.05から0.10あたりにピークがあります。このことから層化抽出によって全体的にみても共変量のバランスが取れていることがわかります。

さらに特徴的なのが再ランダム化（rerandomize）の分布です。そうなるように調整をしているので当然ではあるのですが、1000回繰り返したデータ全てが0.05以下に集中しています。

「サイコロを振り直す」ことによって強制的に共変量の距離を小さくできることがわかりました。

共変量の距離が小さくなることで、当初の課題であった偽陽性が改善しているのかを検証してみましょう。
ただし、この確認は今回の再ランダム化のメリットを直感的に理解するための手続きであることにご留意ください。冒頭と同じ要領で、1000回データ生成とランダム化推論を繰り返しp値の分布を描画しています。図をみると分布が右側にシフトしている、かつ小さなp値を取らなくなっており、差があると判断するような偽陽性のケースが減っています。別の言い方をすると、再ランダム化によって小さなp値をとるようなケースを事前に除外することができた、とも言えるでしょう。

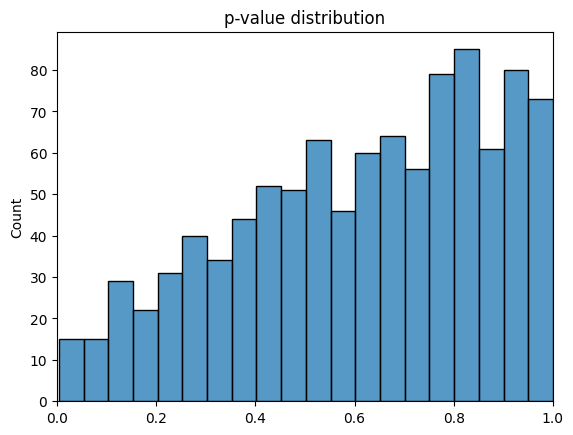
この図のトリックは、ランダム化推論を行う際に任意の割り付け集合を比較対象にしている部分にあります。この手続きは、実際の効果検証の場面では保守的な推論をしてしまう可能性があります。再ランダム化した際の適切な検定方法や具体的な手続きについては[Morgan and Rubin 2012]や [Zhu and Liu 2023] などが詳しいです。

まとめと予告

ABテストにおける偽陽性を減らすために実験設計そのものを工夫するというアプローチに焦点をあてました。今回は、事前に共変量バランスを改善する方法を検討し、層化抽出と再ランダム化が有効であることを確認しました。

今回の試したデータのケースでは再ランダム化は強制的に共変量バランスを制御できそうでした。

一方で、ここまで読まれた方は再ランダム化について以下のような疑念が浮かんでいるかもしれません。

ランダム化を繰り返すのは計算時間の観点でも効率が悪いのではないか？
欲しい結果がでるまで何度もランダム化するのは本当にランダムな実験になっているのか？

これらの疑問や課題に対してのアプローチは実は近年も継続して論文誌などで発表されている内容になります。近日中にこれらの議論を交えた第二回のブログを投稿できればと思います。

参考文献

[Deaton and Cartwright, 2018] Deaton, Angus, and Nancy Cartwright. “Understanding and misunderstanding randomized controlled trials.” Social science & medicine 210 (2018): 2-21.

[Morgan and Rubin 2012] Morgan, Kari Lock, and Donald B. Rubin. “Rerandomization to improve covariate balance in experiments.” (2012): 1263-1282.

[Johansson et, al. 2021] Johansson, P., Rubin, D. B., & Schultzberg, M. (2021). On optimal rerandomization designs. Journal of the Royal Statistical Society Series B: Statistical Methodology, 83(2), 395-403.

[Zhu and Liu 2023] Zhu, K., & Liu, H. (2023). Pair‐switching rerandomization. Biometrics, 79(3), 2127-2142.

[Cunningham 2021] Cunningham, S. (2021). Causal inference: The mixtape. Yale university press. （邦訳：Scott Cunningham (2023) 『因果推論入門〜ミックステープ：基礎から現代的アプローチまで』加藤真大 [ほか] 訳, 技術評論社）

[Imbens and Rubin 2015] Causal inference in statistics, social, and biomedical sciences. Cambridge university press. （邦訳：G.W. インベンス, D. B. ルービン (2023)『インベンス・ルービン統計的因果推論』星野崇宏・繁桝算男監訳）

注釈

*1 全く差がない状況で有意と判断されない確率が0.95であり1 – 0.95^47 = 0.91 と算出

*2 筆者は社会科学、医学、疫学で使われるのが共変量、機械学習の文脈で使われるのが特徴量、くらいのラフな使い分けをしています。

*3 一般的なマハラノビス距離はこの定義に平方根を取ったもので定義されることが多いですが、[Morgan and Rubin 2012]を含む、再ランダム化の分野の慣習に従いこの定義で議論を進めます。

管理画面にWasm入れてみた

『呪術廻戦ファントムパレード』ストーリー制作を支えるグラフィックシステム