はじめに
2023年12月から4ヶ月ほど、協業リテールメディアdiv.にてインターンシップをしていました。早稲田大学大学院2年の澤木陽人です。
大学院ではパターン認識や機械学習を専攻しており、インターンでもML/DS職として参加しました。
本記事はインターンシップで行ったことのまとめ 第二弾となっております。
配属部署のアプリ運用カンパニーの説明は第一弾の記事で紹介していますので、詳しくはそちらをご覧ください。
本記事では、私が取り組んだ論文実装に関してその解説をまとめます。
分析の精度と確度への取り組みの重要性
私が配属されたアプリ運用カンパニーには、多くのデータサイエンティストが在籍しており、日々さまざまな分析や示唆が出されています。広告配信の効果を分析することは、次の意思決定に繋がるだけでなく、提供価値の裏付けにもなるため、私が所属するチームにとって非常に価値のあるタスクでした。
そこで、分析の上で重要となるのが、推定の精度と確度(分散の小ささ)です。
正しい推定値は得られるのか、そしてそれがどれだけ曖昧さがなく推定できるのか、これは統計的推測の観点でとても重要です。
AI Labから提案された一本の論文
第一弾の記事にも書いた通り、私はまさに広告効果をいかによく検出するかに悪戦苦闘していました。
そこで、AI Labに所属し首席データサイエンティストでもある安井翔太さんから次の論文を活用してみたらどうかという提案をいただきました。
Machine Learning for Variance Reduction in Online Experiments Yongyi Guo, et al., NeurIPS 2021
この論文は、タイトルの通り機械学習を用いた分散削減手法です。
本論文の背景を本文中から要約すると
「オンライン実験では、サンプルサイズは大きくても最小検出可能効果サイズが小さく、興味のあるアウトカムの分散が大きくなってしまうことがある。これらの設定において、分散削減法は、より少ないデータで正確な推論を可能にする必要がある」
と述べられており、これは私が取り組んでいた広告効果の分析にもってこいの手法だと確信しました。
広告効果の分析では、ユーザー集合全体は十分に大きいが購買ユーザー自体は比較的小さく、推定値の分散が大きくなってしまいがちだからです。
このような経緯で、この論文の提案手法(以下、論文内での呼称を引用しMLRATEと呼ぶ)の実装を行いました。
効果検証の基本
MLRATEの説明をする前に、効果検証の枠組みについて簡易的な説明をしておきます。
この辺りの知識がすでにある方は読み飛ばしていただいて構いません。
通常、効果検証の手続きでは、何かしらの介入があった場合となかった場合に、効果を測定したい指標にどれだけの差が生じるかを推定します。今回ここでいう介入とは広告の配信にあたり、測定指標は実際に購買するかどうかです。
すなわち、広告に当たった場合と当たらなかった場合に、購買率がどれほど変わるか(処置効果)をデータから推定することになります。
しかし、同じユーザーが「広告が配信された・されなかった」の両方を経験することはできず、真の処置効果はわかりません。そこで、介入があったユーザーグループ(処置群)と、介入のなかったユーザーグループ(対照群)を比較することによって、処置効果を推定します。
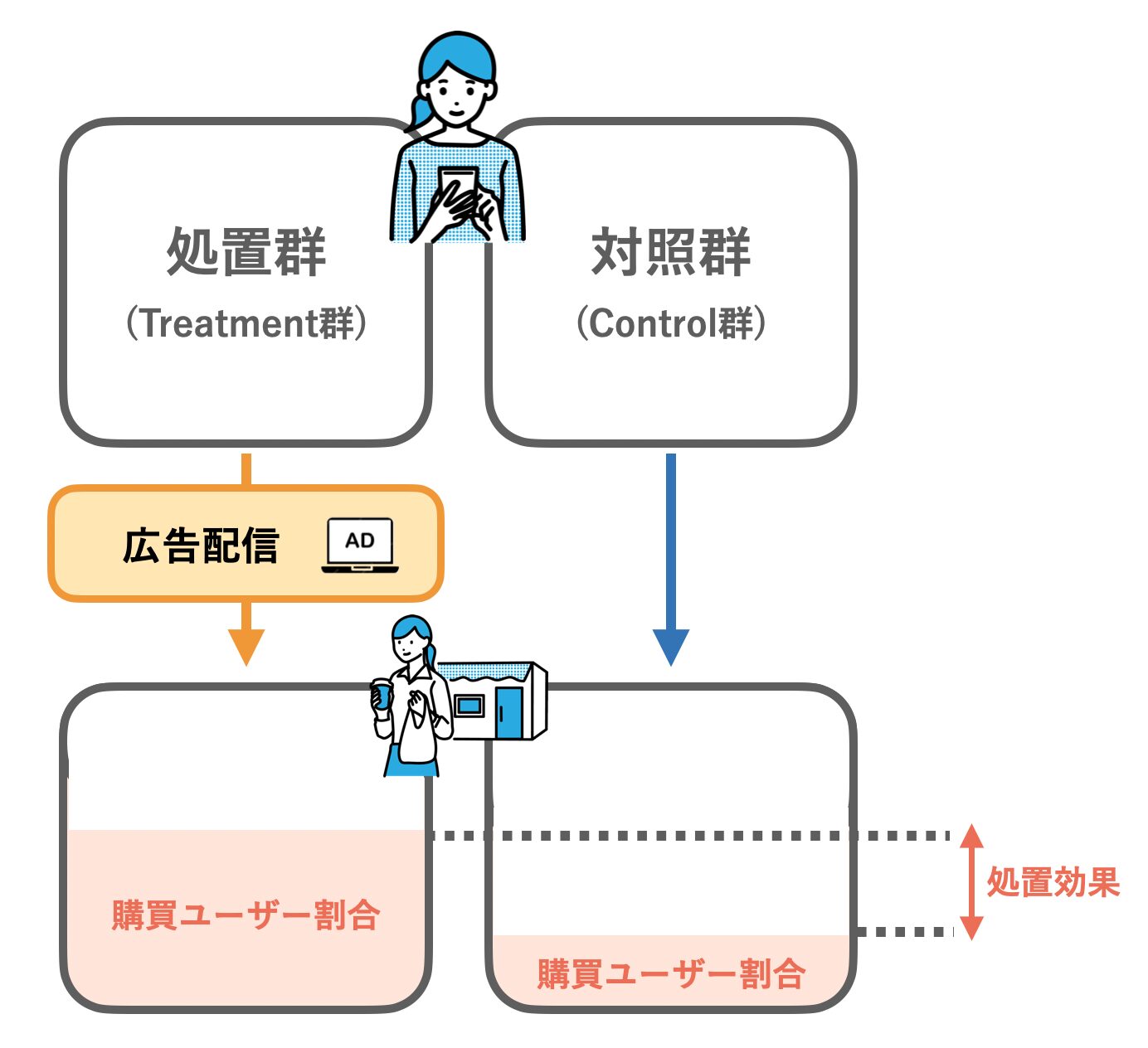
ユーザーが処置群/対照群のどちらに属するかをT=1/0とし、結果的に購買したか否かをY=1/0とすれば、両群のYの平均を比較して、平均的な処置効果を推定できます。
式で見ると以下のようになります。
$$E[Y(T=1)−Y(T=0)]=E[Y|T=1]–E[Y|T=0] $$
これはTで条件付けられた平均の差であるため、次の単回帰におけるTの係数c_1に一致します。
$$Y=c_0+c_1T$$
これが処置効果の基本的な推定方法となります。
なお、このようにユーザーを2群に分けてその差を検証する際、それぞれの群に割り振られるユーザーの特徴は、介入の有無を除いて均質であるべきです(RCT; ランダム化比較試験)。
例えば、購入歴のほとんどないユーザーが処置群にばかり割り振られると、広告にあたっても消費行動につながらず、平均的な処置効果が実際より低く推定されてしまうかもしれません。
このようなバイアスを避けるべく、私の配属部署では、より均質なグループ分けを行うための取り組みも行なっています。興味のある方はぜひ次の記事も併せてご覧ください。
サイコロを振り直す:ABテストにおける共変量バランス調整の検討①
MLRATEの手法
本題のMLRATEについて説明していきます。
MLRATEで提案されている手法は比較的シンプルで、実装も難しくありません。大雑把にまとめると以下のようになります。
- (アウトカムY、共変量X、処置の有無T)からなるデータセットをk個の集合に分割する
- 各分割において、残りのデータから機械学習モデル\(Y=g(X)\)を学習する
- モデルの予測値を含んだ線形モデル(赤い部分)で回帰する
- 回帰値\(\alpha_1\)を平均処置効果とし、その信頼区間を計算する

論文より引用
より詳細に手法の流れをみていきましょう。
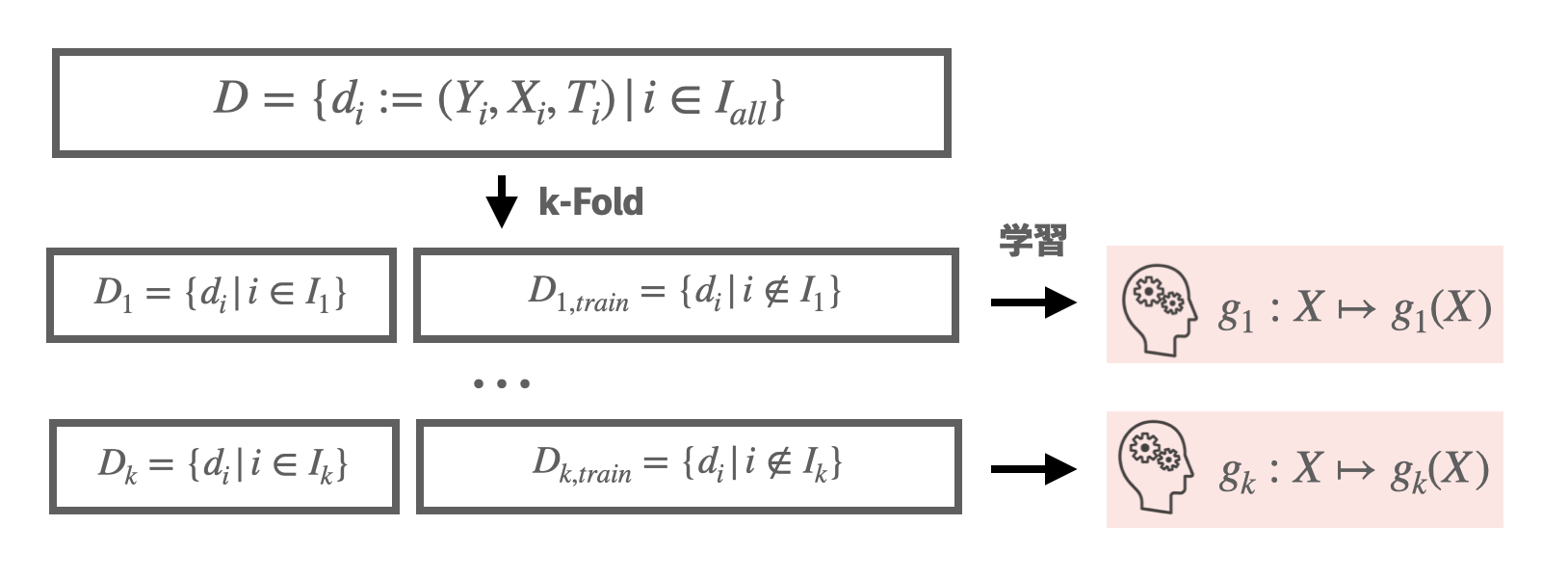
Step1. 交差検証による学習
まずはじめに、交差検証のためにデータセットを複数の小さなデータセットへと分割します。
これは通常の交差検証と変わりなく、過学習の影響を避け汎化性能を向上させる目的で導入されています。
訓練データはモデルgがデータに過剰に適合するため、g(X)がYにほぼ一致してしまいます。これは次のステップの処置効果の回帰において共変量にYを用いるような状況になってしまい、これは処置効果の正しい推定ができません。
交差検証を行うことで、訓練データへのリーク無しに各々の予測値を回帰で用いることができます。
どうやら機械学習モデルY=g(X)に求められているのは、Yをドンピシャで当てるというよりかは、データ全体の傾向を捉えることで、共変量Xに対して妥当なYの値を推定することのようです。
Step2. 処置効果の回帰
各データの共変量Xに対してYの予測値g(X)が求まれば、それを用いて平均処置効果の検証を行います。
ここでデータセット全体に対して、全ての予測値の平均\(\bar{g}\)を計算しておきます。ただし\(X_i\)の予測を行うモデルを\(g_{k(i)}(・)\)と略記しています。
\begin{equation}
\bar{g} = \frac{1}{N} \Sigma_{i}^{N}g_{k(i)}(X_i)
\end{equation}
そして肝心の回帰式は次の通りです。
\begin{equation}
Y_i = \alpha_0 + \alpha_1 T_i + \alpha_2 g_{k(i)}(X_i) + \alpha_3 T_i \left( g_{k(i)}(X_i) – \bar{g} \right) + \epsilon_i
\end{equation}
- \(Y_i\) : アウトカム
- \(T_i\) : 処置の有無(処置群に割り当てられた場合は1、対照群に割り当てられた場合は0)
- \(g_{k(i)}(X_i)\) : 共変量 \(X_i\) からの機械学習モデルの予測値
- \(\bar{g}\) : すべての予測値の平均
- \(\alpha_0\), \(\alpha_1\), \(\alpha_2\), \(\alpha_3\) : 回帰係数 \(\epsilon_i\) : 誤差項
この \(\alpha_1\)の回帰値が平均処置効果の推定値となります。
やや複雑な形をしているので、各項の意図するところを解説しておきます。
回帰式の各項の役割
1. 定数項 \((\alpha_0)\):
・回帰モデルの切片
2. 処置効果項 \((\alpha_1 T_i)\):
・処置を受けた場合の平均的な効果量
・他の共変量に相関して変化するような異質性はこの項では捉えない
3. 予測値による調整項 \((\alpha_2 g_{k(i)}(X_i))\):
・機械学習モデル g_kの予測値による調整項
・共変量 X_iから求まった予測値g(X)とアウトカム Y_iの関係をモデル化する
4. 交互作用項 \((\alpha_3 T_i (g_{k(i)}(X_i) – \bar{g}))\):
・処置と予測値の交互作用項
・処置があった場合の予測値平均からの乖離の異質性を捉える
5. 誤差項 \((\epsilon_i)\):
・モデルが説明できない残差
これらの回帰式によって、それぞれの群において、データが次の直線にフィッティングされることになります。
\begin{array}{|l|l|l|} \hline \quad\quad\quad\quad & \text{対照群 (T=0)} & \text{処置群 (T=1)} \\ \hline \alpha\text{の回帰式} & Y = \alpha_0 + \alpha_2 g(X) & Y = (\alpha_0 + \alpha_1 – \alpha_3 \bar{g}) + (\alpha_2 + \alpha_3) g(X) \\ \hline \end{array}

Step3. 分散の計算・信頼区間の構成
信頼区間を計算するにはまずは分散を求めなくてはなりません。
平均処置効果の推定値\(\alpha_1\)の分散は、\( \hat{p} := \sum_i T_i / N \)を処置群の割合として、次で求めることができます。
\begin{equation}
\hat{\sigma}_{\alpha_1}^2 = \frac{\text{Var}(Y_i | T_i = 0)}{1 – \hat{p}} + \frac{\text{Var}(Y_i | T_i = 1)}{\hat{p}} – \frac{\text{Var}(g_{k(i)}(X_i))}{\hat{p}(1 – \hat{p})} \left[ \beta_2(\{g_k\}_{k=1}^K)\hat{p} + \left( \beta_2(\{g_k\}_{k=1}^K) + \beta_3(\{g_k\}_{k=1}^K) \right)(1 – \hat{p}) \right]^2
\end{equation}
この右辺の第3項がまさにMLRATEによって分散削減を達成する部分にあたります。
初登場の \(\beta_i(\{g\}_{k=1}^{K})\) が入っていますが、これについては長くなるので次の節で補足することにします。
以上で計算された標本分散 \(\hat{\sigma}_{\alpha_1}^2\) は、十分なサンプル数のもとで母分散に確率収束することが論文中で示されています。
\(\alpha_1\) は \(\sqrt{N} \left( \hat{\alpha}_1 – \alpha_1 \right) \sim N(0, \sigma_{\alpha_1}^2)\) に漸近的に従うため、信頼区間は次のように計算されます。
\begin{equation}
\hat{\alpha}_1 \pm \Phi^{-1}_{(1 – \alpha/2) }\frac{\hat{\sigma}_{\alpha_1}}{\sqrt{N}}
\end{equation}
ここで、\(\Phi^{-1}_{(\cdot)}\)は標準正規分布の累積分布関数の逆関数です。
以上がMLRATEの手法の一連の流れとなります。

(補足1) \(\beta_i \)の計算
分散の削減項の中に突如現れた \(\beta_i(\{g_k\}_{k=1}^K)\) は別途計算しておく必要があります。
結論から述べると、\(\beta_i\) は次の回帰式から求まる回帰係数です。(論文中ではモデル g との依存関係を表すために \(\beta_i(\{g_k\}_{k=1}^K)\) と表記されていますが、以後省略します。)
\begin{equation}
Y_i = \beta_0 + \beta_1 T_i + \beta_2 g(X_i) + \beta_3 T_i g(X_i) + \epsilon_i
\end{equation}
MLRATEの回帰式によく似ていますが、こちらは第3項においてモデル予測値の平均値が引かれていない点に注意してください。
この回帰によって、データはそれぞれ次の直線にフィッティングされます。
\begin{array}{|l|l|l|} \hline \quad\quad\quad\quad & \text{対照群 (T=0)} & \text{処置群 (T=1)} \\ \hline \beta\text{の回帰式} & Y_i = \beta_0 + \beta_2 g(X_i) + \epsilon_i & Y_i = (\beta_0 + \beta_1) + (\beta_2 + \beta_3) g(X_i) + \epsilon_i \\ \hline \end{array}
ここで、本題のMLRATE回帰式で求められる平均処置効果\(\alpha_1\)は\(\beta_i\)と理想的には次の関係に収束することが期待できます。
\begin{equation}
{\alpha}_1 = {\beta}_1 + {\beta}_3 \bar{g}
\end{equation}
これは、平均処置効果を平均的なモデル予測値から生じる異質性の影響を織り込んで補正していると解釈できます。
(補足2) 理論的にはどの程度分散が削減できるのか?
実際、MLRATEを使ってどの程度分散が削減できるのでしょうか。
平均処置効果\(ATE=E[Y|T=1]-E[Y|T=0]\)は単回帰\(Y=c_0+c_1T\)の回帰値\(c_1\)に一致するため、処置群の割合をpとすればATEの分散は
\begin{equation}
\sigma^2_{c_1}= \frac{Var(Y|T=1)}{p}+ \frac{Var(Y|T=0)}{1-p}
\end{equation}
となります。一方でMLRATEの手法で求めたATEの分散は、前述の通り、
\begin{equation}
\sigma_{\alpha_1}^2 = \frac{\text{Var}(Y_i | T_i = 0)}{1 – \hat{p}} + \frac{\text{Var}(Y_i | T_i = 1)}{\hat{p}} – \frac{\text{Var}(g_{k(i)}(X_i))}{\hat{p}(1 – \hat{p})} \left[ \beta_2(\{g_k\}_{k=1}^K)\hat{p} + \left( \beta_2(\{g_k\}_{k=1}^K) + \beta_3(\{g_k\}_{k=1}^K) \right)(1 – \hat{p}) \right]^2
\end{equation}
であるため、分散の削減は第3項の大きさにのみに依存することがわかります。実際に式を書き下すと、相対的な分散の削減効果は次のように書き換えられます。
\begin{equation}
\frac{\sigma^2_{\alpha_1}}{\sigma^2_{c_1}}=1-\Bigr(Corr(Y,g(X))\Bigr)^2
\end{equation}
すなわち、機械学習モデル\(g\)の\(Y\)に対する予測\(g(X)\)がよく相関しているほど分散削減効果が大きくなります。
例えば予測精度が相関係数にして0.50のモデルを用いれば理論的にはATEの信頼区間が約13.4%削減できることになります。
なお、高い予測精度のモデルを構築できれば、以上の理由から高い分散削減効果を得られますが、過学習を起こしてしまうと処置効果自体の推定に悪影響を及ぼすため注意が必要です。
トイデータによる実験
実際にMLRATEの効果を実験してみましょう。
業務で扱った実際のデータを用いるわけにはいかないため、ここではKaggleのデータセットを使います。
広告に当たったか否か\((T=0/1)\)、実際に購買したか\((Y=0/1)\)、その他の共変量\((X)\)が含まれているため、MLRATEの検証が可能です。
https://www.kaggle.com/datasets/faviovaz/marketing-ab-testing
データセットの内容
与えられたデータセットの簡単な説明をしておきます
- user id:ユーザーのID(一意)
- test group:”ad”=広告を見た, “psa”=公共広告のみを見た
- converted:”True”:製品を購入、”False”:購入していない
- total ads:その人が見た広告の総数
- most ads day:その人が最も多く広告を見た日(Sunday, Monday, …, Saturday)
- most ads hour:その人が最も多く広告を見た時間帯(0,1,…,23)
データに含まれる各ユーザーグループの大きさは次のとおりです。
\begin{array}{|l|l|l|l|} \hline \text{項目} & \text{全体}\quad\quad & \text{処置群(T=1)} & \text{対照群(T=0)} \\ \hline \text{データサイズ} & 588181 & 564577 & 23524 \\ \text{CV人数(Y=1)} & 14843 & 14423 & 420 \\ \hline \end{array}
前処理
データの欠損もない非常にシンプルなデータなため最低限の前処理だけ行いました。
- test group:\(T=0/1\)として2値化
- most ads day:one-hot encoding
- most ads hour : \((\sin(2πx/24), \cos(2πx/24))\)で周期性データに変換
モデルの学習
LightGBMを使って5-Foldで学習を行います。
損失にはRMSEを用い、過学習を防ぐため浅めのモデルで学習を行いました。
データ全体に対してCVユーザー(Y=1)は多くないため、学習時には\(Y=1/0\)の比率を4:1でunder samplingし、さらにモデルのcalibrationを行なっています。

Y=0/1の予測分布
精度は、\(Y\)と\(g(X)\)の相関ベースで0.28でした。凝ったことをしていないので精度は微妙です。
MLRATEの適用
まずは、\((1, T, g(X), T(g(X)-\bar{g}))\)の組を用いて回帰を行います。
\begin{equation}
Y_i = \alpha_0 + \alpha_1 T_i + \alpha_2 g_{k(i)}(X_i) + \alpha_3 T_i \left( g_{k(i)}(X_i) – \bar{g} \right) + \epsilon_i
\end{equation}
\begin{array}{|l|l|l|l|l|l|l|} \hline \text{Coefficient} & \text{Estimate Coef.}\quad & \text{Std. Error}\quad & \text{t-value}\quad & \text{p-value}\quad & [0.025\quad & 0.975]\quad \\ \hline \alpha_0: \text{const} & -0.0021 & 0.001 & -1.715 & 0.086 & -0.005 & 0.000 \\ \alpha_1: T & 0.0079 & 0.001 & 7.847 & 0.000 & 0.006 & 0.010 \\ \alpha_2: g(X) & 0.1579 & 0.006 & 26.800 & 0.000 & 0.146 & 0.169 \\ \alpha_3: T*(g(X)-g_{AVE}) & 0.1135 & 0.006 & 18.854 & 0.000 & 0.102 & 0.125 \\ \hline \end{array}
Tの係数が平均処置効果ATEにあたります。値は\(\alpha_1 = 0.007862\)でした。
データセットから単純に計算される平均処置効果は\(c_1=0.007692\)なので、推定値はおよそ問題ないように思えます。
次に、信頼区間の推定を行います。(1, T, g(X), T(g(X)))に対して同様に回帰を行います。
\begin{equation}
Y_i = \beta_0 + \beta_1 T_i + \beta_2 g(X_i) + \beta_3 T_i g(X_i) + \epsilon_i
\end{equation}
\begin{array}{|l|l|l|l|l|l|l|} \hline \text{Coefficient} & \text{Estimate Coef.}\quad & \text{Std. Error}\quad & \text{t-value}\quad & \text{p-value}\quad & [0.025\quad & 0.975]\quad \\ \hline \beta_0: \text{const} & 0.0021 & 0.001 & 1.859 & 0.063 & -0.000 & 0.004 \\ \beta_1: T & -0.0029 & 0.001 & -2.482 & 0.013 & -0.005 & -0.001 \\ \beta_2: g(X) & 0.6190 & 0.023 & 27.437 & 0.000 & 0.575 & 0.663 \\ \beta_3: T*g(X) & 0.4238 & 0.023 & 18.398 & 0.000 & 0.379 & 0.469 \\ \hline \end{array}
よって、\(\beta\)の推定値は以下のようになりました。
\begin{equation}
\boldsymbol{\beta} = \begin{pmatrix}
\beta_0 \\
\beta_1 \\
\beta_2\\
\beta_3
\end{pmatrix}=
\begin{pmatrix}
2.11e-03 \\
-2.88e-03 \\
6.19e-01\\
4.24e-01
\end{pmatrix}
\end{equation}
これを用いて、分散および信頼区間を計算します。
\begin{align*}
\hat{\sigma}_{\alpha_1}^2 &= \frac{\text{Var}(Y_i | T_i = 0)}{1 – \hat{p}} + \frac{\text{Var}(Y_i | T_i = 1)}{\hat{p}} – \frac{\text{Var}(g_{k(i)}(X_i))}{\hat{p}(1 – \hat{p})} \left[ \beta_2(\{g_k\}_{k=1}^K)\hat{p} + \left( \beta_2(\{g_k\}_{k=1}^K) + \beta_3(\{g_k\}_{k=1}^K) \right)(1 – \hat{p}) \right]^2 \\
&= 0.0259 + 0.4384 – 0.0194 \\
&= 0.4449
\end{align*}
\begin{equation}
CI_{\alpha_1}=\hat{\alpha}_1 \pm \Phi^{-1}_{(1 – 0.05/2) }\frac{\hat{\sigma}_{\alpha_1}}{\sqrt{N}}= 0.7862 ± 0.195\%=\Bigr[0.5913\%, 0.9812\% \Bigr]
\end{equation}
MLRATEによる調整を行わない場合の信頼区間は
\begin{equation}
CI_{c_1}= 0.7692 ± 0.205\%=\Bigr[0.5647\%, 0.9738\% \Bigr]
\end{equation}
であるため、信頼区間が4.9%ほど削減できました。
今回使用したモデル予測値\(g(X)\)のアウトカムとの相関は0.28であったため、信頼区間は理論的には4.0%程度削減されることなり、およそこれに従ったと言えそうです。
実務への展望
MLRATEが確度の高い効果検証を可能にすることがわかりました。しかし、その分散削減効果を最大限に引き出すには、汎化性能が高く、精度の高い予測モデルが必要です。
現在、配属部署では、効率の良い広告配信を目指し、購買しそうなユーザーを予測する「AIセグメント」と呼ばれるモデルを開発・運用しています。このモデルとMLRATEを組み合わせることで、さらに効果的な活用が期待できるかもしれません。
さらに、MLRATEはアウトカムYを予測するモデルに制約がないため、説明変数の形式を問いません。これにより、通常の効果検証では扱いにくいセンシングデータや画像データなどもモデルの学習に利用することができます。アプリ運用センターには多様なデータが蓄積されているため、このような新しいアプローチも実務での活用が考えられます。
おわりに
第一弾のブログでも書いたように、チーム全体でより良い意思決定のための分析を行う雰囲気が醸成されており、とても素晴らしい経験をさせていただきました。
メインのタスクの傍ら、安井さんの一声で始まったMLRATEの実装ですが、効果検証に関する非常に良い勉強になったと実感しています。
知識・技術共に至らぬ点も多かった中、優しく支えてくださったトレーナーの河野さん、メンターの青見さん、早川さん、須ヶ﨑さんを初め、安井さんをはじめとするAI Lab皆様、そしてチームの皆様、本当にありがとうございました!
